Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$

Tọa độ tâm I là:
x=(4-2)/2=1 và y=(-1+5)/2=2
I(1;2); A(4;-1)
\(IA=\sqrt{\left(4-1\right)^2+\left(-1-2\right)^2}=3\sqrt{2}\)
=>Phương trình đường tròn là:
(x-1)^2+(y-2)^2=18

`BC = \sqrt((4-2)^2+(3+1)^2) = 2\sqrt5`
`=> R=(BC)/2= \sqrt5`
`=> (C): (x-1)^2+(y-2)^2=5`

a.
\(\overrightarrow{AB}=\left(-6;3\right)\Rightarrow AB=\sqrt{\left(-6\right)^2+3^2}=3\sqrt{5}\)
Đường tròn (C) tâm A và đi qua B có bán kính \(R=AB=3\sqrt{5}\)
Phương trình:
\(\left(x-3\right)^2+\left(y-1\right)^2=45\)
b.
Gọi M là trung điểm AB \(\Rightarrow M\left(0;\dfrac{5}{2}\right)\)
Đường tròn đường kính AB có tâm M và bán kính \(R=\dfrac{AB}{2}=\dfrac{3\sqrt{5}}{2}\)
Phương trình:
\(x^2+\left(y-\dfrac{5}{2}\right)^2=\dfrac{45}{4}\)

Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t

a: \(AB=\sqrt{\left(-3-1\right)^2+\left(6-2\right)^2}=\sqrt{4^2+4^2}=4\sqrt{2}\)
Phương trình đường tròn (C) là:
\(\left(x-1\right)^2+\left(y-2\right)^2=\left(4\sqrt{2}\right)^2=32\)
b: Gọi I là trung điểm của AB
Tọa độ I là:
\(\left\{{}\begin{matrix}x=\dfrac{1+\left(-3\right)}{2}=-\dfrac{2}{2}=-1\\y=\dfrac{2+6}{2}=\dfrac{8}{2}=4\end{matrix}\right.\)
vậy: I(-1;4)
I(-1;4); A(1;2)
=>\(IA=\sqrt{\left(1+1\right)^2+\left(2-4\right)^2}=2\sqrt{2}\)
Phương trình đường tròn tâm I, bán kính IA là:
\(\left[x-\left(-1\right)\right]^2+\left(y-4\right)^2=IA^2\)
=>\(\left(x+1\right)^2+\left(y-4\right)^2=8\)

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
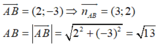
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
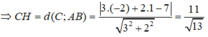
Diện tích tam giác ABC là:
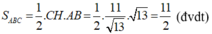
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
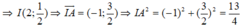
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
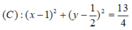
\(\overrightarrow{AB}=\left(6;-2\right)\Rightarrow AB=2\sqrt{10}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;4\right)\)
ĐƯờng tròn (C) nhận I là tâm và có bán kính \(R=\dfrac{AB}{2}=\sqrt{10}\)
Phương trình: \(\left(x-1\right)^2+\left(y-4\right)^2=10\)