
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

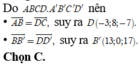

làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
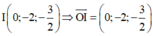
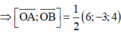
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào