Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

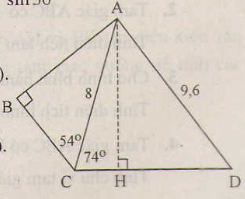
a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Vì ΔABH vuông tại H(gt)
Mà: \(\widehat{ABC}=45\left(gt\right)\)
=>ΔABH vuông cân tại H
=>BH=AH=8cm
Xét ΔAHC vuông tại H(gt)
=> \(AC^2=AH^2+HC^2\) (theo đl pytago)
=>\(AC^2=8^2+25^2=289\)
=>AC=17cm

Tam giác vuông có các tỉ số cạnh tỉ lệ với sin, cos, tan
ví dụ \(A B = 8\), \(A C = 15\)
\(B C = \sqrt{8^{2} + 15^{2}} = 17\)
Vì tam giác vuông này có tỉ số \(\frac{A C}{A B} = \frac{15}{8}\) ta tra bảng hoặc dùng máy tính để tìm góc \(B \approx 61 , 9^{\circ}\)
Rồi \(\angle C = 28 , 1^{\circ}\)
a.
\(C=90^0-B=90^0-38^0=52^0\)
\(BC=\frac{AB}{\cos B}=\frac{20}{\cos38^0}=25,38\operatorname{cm}\)
\(AC=AB.\tan B=20.\tan38^0=15,63\operatorname{cm}\)
b.
\(B=90^0-C=90^0-54^0=36^0\)
\(BC=\frac{AC}{\cos C}=\frac{25}{\cos54^0}=42,53\operatorname{cm}\)
\(AB=AC.\tan C=25.\tan54^0=34,41\operatorname{cm}\)
c.
\(C=90^0-B=23^0\)
\(AB=BC.\cos B=10,94\operatorname{cm}\)
\(AC=BC.\sin B=25,77\operatorname{cm}\)
d.
Ap dung Pitago:
\(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{8^2+15^2}=17\operatorname{cm}\)
\(\sin B=\frac{AC}{BC}=\frac{15}{17}\Rightarrow B=61^055^{\prime}\)
\(C=90^0-B=28^05^{\prime}\)
e.
Ap dung Pitago:
\(AB^2+AC^2=BC^2\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{21^2-10^2}=\sqrt{341}cm\)
\(\cos B=\frac{AB}{BC}=\frac{10}{21}\Rightarrow B=61^034^{\prime}\)
\(C=90^0-B=28^026^{\prime}\)

Hãy tích cho tui đi
khi bạn tích tui
tui không tích lại bạn đâu
THANKS

Ta có:
\(x^4+4=\left(x^4+4x^2+4\right)-4x^2\)
=\(\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2+2x+2\right)\left(x^2-2x+2\right)\)
=> \(x^4+4\) chia hết cho \(x^2+2x+a\) khi \(\left(x^2+2x+2\right)\left(x^2-2x+2\right)⋮\left(x^2+2x+a\right)\)
=> a = 2.
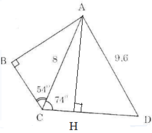
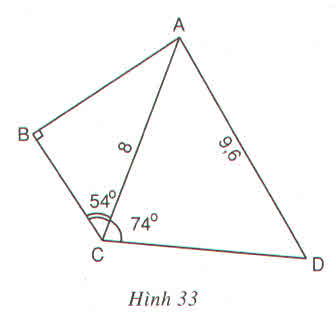



Trong tam giác ACD, kẻ đường cao AH.
Ta có: AH = AC . sinACH = 8.sin74o 7,69 (cm)