Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t-\dfrac{2\pi x}{\lambda}\right)\)
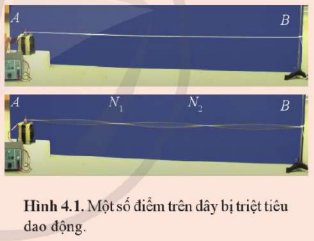
Khoảng cách giữa hai điểm gần nhau nhất dao động cùng pha là λ và khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \(\dfrac{\lambda}{2}\)

Từ phương trình \(x = 5 sin \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right)\) (cm)
\(\Rightarrow A = 5\) cm; \(\omega = 2 \pi\) rad/s
Ta có: \(\text{v} = x^{'} = \omega A cos \left(\right. \omega t + \varphi \left.\right) = 2 \pi . 5. cos \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right) = 10 \pi cos \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right)\) cm/s
a. Ở thời điểm \(t = 5\) s
Ta có: \(x = 5 sin \left(\right. 2 \pi . 5 + \frac{\pi}{6} \left.\right) = 2 , 5\) cm
\(\text{v} = 10 \pi cos \left(\right. 2 \pi . 5 + \frac{\pi}{6} \left.\right) = 5 \sqrt{30}\) cm/s
\(a = - \omega^{2} x = - \left(\left(\right. 2 \pi \left.\right)\right)^{2} . 2 , 5 = - 100\) cm/s2
b. Khi pha dao động là 120o.
\(x = 5 sin 12 0^{o} = 2 , 5 \sqrt{3}\) cm
\(v = 10 \pi cos 12 0^{o} = - 5 \pi\) cm/s
\(a = - \omega^{2} x = - 4 \pi^{2} . 2 , 5 \sqrt{3} = - \sqrt{3}\) cm/s2

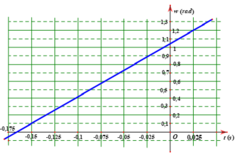
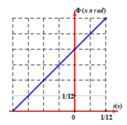
a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)

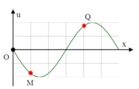
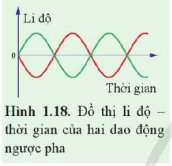
Hai dao động đều có chu kì `T` và thời điểm `t=0` tại vị trí cân bằng, nhưng tại cùng thời điểm tiếp theo thì:
- Dao động màu xanh đến biên dương.
- Dao động màu hồng đến biên âm.
Mà từ biên dương đến biên âm chênh lệch 1 góc `\pi`.
`=>` Độ lệch pha của hai dao động là: `\pi (rad)`
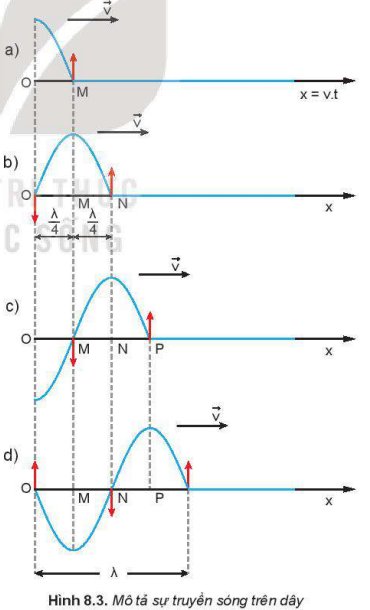


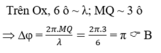
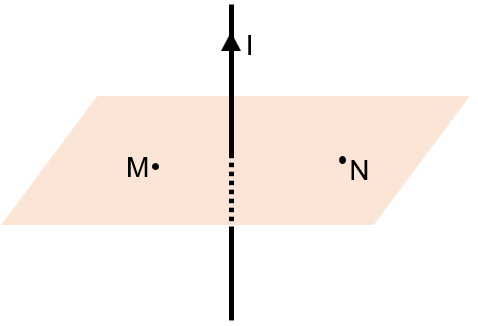

Từ đồ thị ta có thể thấy điểm M đang ở lõm sóng (tạm gọi là biên âm), điểm N đang ở VTCB, điểm P đang ở ngọn sóng (tạm gọi là biên dương).
Nên 2 cặp điểm M và N, N và P dao động lệch pha
Còn điểm M và điểm P dao động ngược pha nhau.