Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\overrightarrow {AB} = \left( {10;5} \right),\overrightarrow {AC} = \left( {6; - 4} \right),\overrightarrow {BC} = \left( { - 4; - 9} \right)\)
+) Đường thẳng AB nhận vectơ \(\overrightarrow {AB} = \left( {10;5} \right)\)làm phương trình chỉ phương và đi qua điểm \(A( - 1;1)\)nên có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 1 + 10t\\y = 1 + 5t\end{array} \right.\)
+) Đường thẳng AC nhận vectơ \(\overrightarrow {AC} = \left( {6; - 4} \right)\)làm phương trình chỉ phương và đi qua điểm \(A( - 1;1)\)nên có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 1 + 6t\\y = 1 - 4t\end{array} \right.\)
+) Đường thẳng BC nhận vectơ \(\overrightarrow {BC} = \left( { - 4; - 9} \right)\)làm phương trình chỉ phương và đi qua điểm \(B\left( {9;6} \right)\)nên có phương trình tham số là: \(\left\{ \begin{array}{l}x = 9 - 4t\\y = 6 - 9t\end{array} \right.\)
b) Ta có vectơ pháp tuyến của hai đường thẳng AB và AC lần lượt là: \(\overrightarrow {{n_1}} = \left( {1; - 2} \right),\overrightarrow {{n_2}} = \left( {2;3} \right)\)
\(\cos \left( {AB,AC} \right) = \cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\left| {1.2 + \left( { - 2} \right).3} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {3^2}} }} = \frac{{4\sqrt {65} }}{{65}} \Rightarrow \left( {AB,AC} \right) = 60^\circ 15'\)
Vậy góc giữa hai đường thẳng AB và AC là \(60^\circ 15'\)
c) Đường thẳng BC nhận vectơ \(\overrightarrow {BC} = \left( { - 4; - 9} \right)\) làm vectơ chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow n = \left( {9; - 4} \right)\) và đi qua \(B\left( {9;6} \right)\), suy ra phương trình tổng quát của đường thẳng BC là:
\(9.\left( {x - 9} \right) - 4\left( {y - 6} \right) = 0 \Leftrightarrow 9x - 4y - 57 = 0\)
Khoảng cách từ \(A( - 1;1)\) đến đường thẳng BC là:
\(d\left( {A,BC} \right) = \frac{{\left| {9.\left( { - 1} \right) - 4.1 - 57} \right|}}{{\sqrt {{9^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{70\sqrt {97} }}{{97}}\)

Tham khảo:
a)
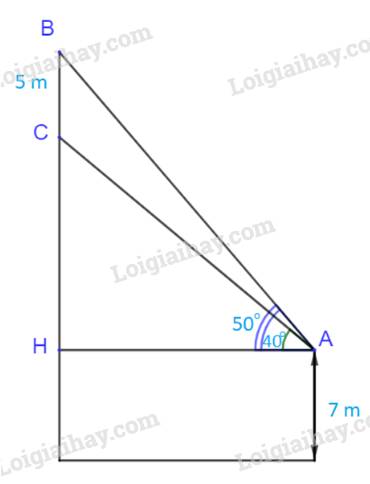
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
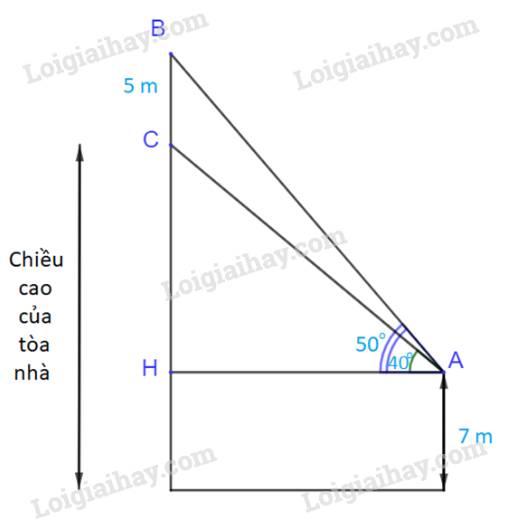
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

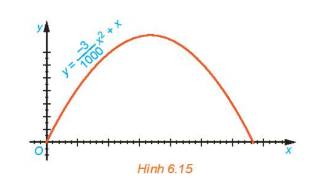
a) Tung độ đỉnh của hàm số \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) là:
\(\frac{{ - \Delta }}{{4a}} = \frac{{ - \left( {{1^2} - 4.\frac{{ - 3}}{{1000}}.0} \right)}}{{4.\frac{{ - 3}}{{1000}}}} = \frac{{250}}{3}\)
Vậy độ cao cực đại của vật là \(\frac{{250}}{3}(m)\)
b) Vật chạm đất khi:
\(y = 0 \Leftrightarrow \frac{{ - 3}}{{1000}}{x^2} + x = 0 \Leftrightarrow x = \frac{{1000}}{3}\)và x=0(loại)
Vậy khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là \(\frac{{1000}}{3}\left( m \right)\)

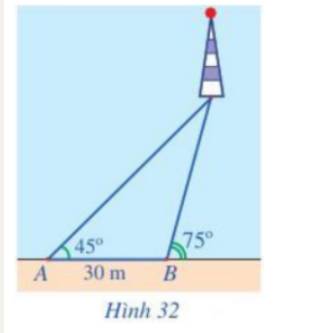
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
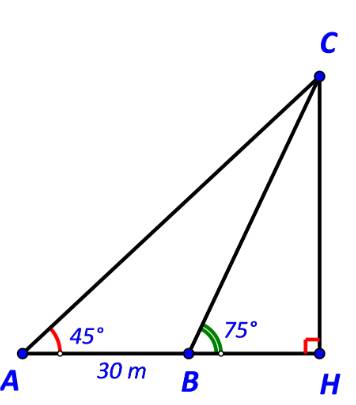
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)

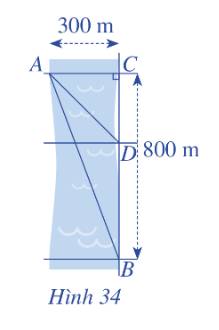
Đổi 300 m =0,3 km, 800 m = 0,8 km
7,2 phút =0,12(h)
Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)
Khi đó, DB=0,8-x (km)
Theo định lý Py-ta-go ta có: \(AD = \sqrt {A{C^2} + C{D^2}} \)\( = \sqrt {0,{3^2} + x^2} \) (km)
Thời gian đi từ A đến D là: \(\frac{{\sqrt {0,{3^2} + x^2} }}{6}\left( h \right)\)
Thời gian đi từ D đến B là: \(\frac{{0,8 - x}}{{10}}\left( h \right)\)
Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:
\(\begin{array}{*{20}{l}}
{\frac{{\sqrt {0,{3^2} + {x^2}} }}{6} + \frac{{0,8 - x}}{{10}} = 0,12}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} + 3.\left( {0,8 - x} \right) = 0,12.30}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} - 3x - 1,2 = 0}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} = 3x + 1,2}\\
{ \Rightarrow 25.\left( {0,{3^2} + {x^2}} \right) = {{\left( {3x + 1,2} \right)}^2}}\\
{ \Leftrightarrow 25.\left( {{x^2} + 0,09} \right) = 9{x^2} + 7,2x + 1,44}\\
{ \Leftrightarrow 16{x^2} - 7,2x + 0,81 = 0}\\
{ \Leftrightarrow x = 0,225 \, \, \, (TM)}
\end{array}\)
Vậy khoảng cách từ vị trí C đến D là 225m.

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

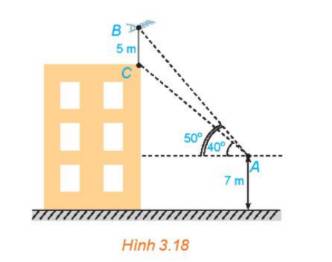

Tham khảo:
Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.
Ta có: \(CD = 27,4 \Rightarrow AC = CD.\sqrt 2 = 27,4.\sqrt 2 \approx 38,75\)
\( \Rightarrow OC = AC - OA \approx 38,75 - 18,44 = 20,31\)
Xét tam giác OCD ta có:
Định lí cos: \(O{D^2} = C{D^2} + C{O^2} - 2.CD.CO.\cos C\)
Trong đó \(\left\{ \begin{array}{l}CD = 27,4\\CO = 20,31\\\widehat C = {45^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow O{D^2} = 27,{4^2} + 20,{31^2} - 2.27,4.20,31.\cos {45^o}\\ \Leftrightarrow O{D^2} \approx 376,255\\ \Leftrightarrow OD \approx 19,4\;(m)\end{array}\)
Dễ thấy \(\Delta \,COB = \Delta \,COD\)(c.g.c) \( \Rightarrow OB = OD = 19,4\;(m)\)