
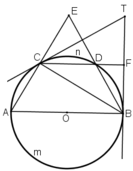
 là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


 là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD


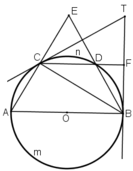
a) + 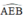 là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 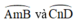
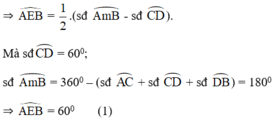
+  là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 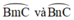


a) Ta có 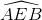 là góc có đỉnh ở bên ngoài đường tròn nên:
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy 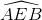 =
=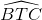
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)

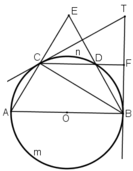
a) + 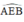 là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 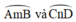
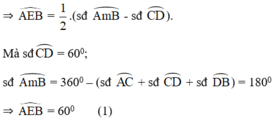
+  là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 

b)  là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

a: Xét ΔOAC có OA=OC và góc AOC=60 độ
nên ΔOAC đều
=>góc CAO=60 độ
Xet ΔOBD có OB=OD và góc DOB=60 độ
nên ΔOBD đều
=>góc B=60 độ
Xét ΔEAB có góc EAB=góc EBA=60 độ
nên ΔEAB đều
=>góc E=60 độ
góc BOC=60+60=120 độ
=>góc BTC=60 độ=góc AEB