
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

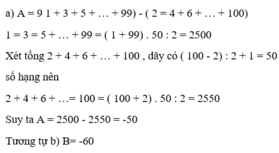

B1a)\(11\frac34-\left(6\frac56-4\frac12\right)+1\frac23\)
=\(11\frac34-6\frac56+4\frac12+1\frac23\)
=\(\left(11-6+4+1\right)+\left(\frac34-\frac56+\frac12+\frac23\right)\)
=\(10+\left(\frac{9}{12}-\frac{10}{12}+\frac{6}{12}+\frac{8}{12}\right)\)
=\(10+\left(-\frac{1}{12}+\frac{6}{12}+\frac{8}{12}\right)\)
=10+\(\frac{13}{12}\)
=\(\frac{120}{12}+\frac{13}{12}\)
=\(\frac{133}{12}\)
b)\(2\frac{17}{20}-1\frac{11}{5}+6\frac{9}{20}:3\)
= \(\frac{57}{20}-\frac{16}{5}+\frac{129}{20}\times\frac13\)
=\(\frac{57}{20}-\frac{16}{5}+\frac{129}{60}\)
=\(\frac{171}{60}-\frac{192}{60}+\frac{129}{60}\)
=\(\frac{108}{60}\)
=\(\frac95\)

S = (1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) + (9 - 10 - 11 + 12) + (13 - 14 - 15 + 16) + (17 - 18)
= 0 + 0 + 0 + 0 + (-1)
= -1
A = (1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) + ... + (2013 - 2014 - 2015 + 2016) + 2017
= 0 + 0 + ... + 0 + 2017
= 2017
S = (1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) +...... + (13 - 14 - 15 + 16)+ 17 - 18
S = 17 - 18 = -2
A = (1 - 2 - 3 + 4) + (5 - 6 -7 + 8) + ..... + (2013 - 2014 - 2015 + 2016) + 2017
A = 2017

2/
S = 2 + 22 + 23 +...+ 299
= (2+22+23) +...+ (297+298+299)
= 2(1+2+22)+...+297(1+2+22)
= 2.7 +...+ 297.7
= 7(2+...+297) chia hết cho 7
S = 2+22+23+...+299
= (2+22+23+24+25)+...+(295+296+297+298+299)
= 2(1+2+22+23+24)+...+295(1+2+22+23+24)
= 2.31+...+295.31
= 31(2+...+295) chia hết cho 31
3/
A = 1+5+52+....+5100 (1)
5A = 5+52+53+...+5101 (2)
Lấy (2) - (1) ta được
4A = 5101 - 1
A = \(\frac{5^{101}-1}{4}\)
4/
Đặt A là tên của biểu thức trên
Ta có: \(\frac{1}{2^2}< \frac{1}{1.2}=\frac{1}{1}-\frac{1}{2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}=\frac{1}{2}-\frac{1}{3}\)
........
\(\frac{1}{8^2}< \frac{1}{7.8}=\frac{1}{7}-\frac{1}{8}\)
\(\Rightarrow A< \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{7}-\frac{1}{8}=\frac{1}{1}-\frac{1}{8}=\frac{7}{8}< 1\)
Vậy...
5/
a, Gọi UCLN(n+1,2n+3) = d
Ta có : n+1 chia hết cho d => 2(n+1) chia hết cho d => 2n+2 chia hết cho d
2n+3 chia hết cho d
=> 2n+2 - (2n+3) chia hết cho d
=> -1 chia hết cho d => d = {-1;1}
Vậy...
b, Gọi UCLN(2n+3,4n+8) = d
Ta có: 2n+3 chia hết cho d => 2(2n+3) chia hết cho d => 4n+6 chia hết cho d
4n+8 chia hết cho d
=> 4n+6 - (4n+8) chia hết cho d
=> -2 chia hết cho d => d = {1;-1;2;-2}
Mà 2n+3 lẻ => d lẻ => d khác 2;-2 => d = {1;-1}
Vậy...

a) 1 - 2 + 3 - 4 + 5 - 6 + .....+ 25 - 26
= (1 - 2) + (3 - 4) + (5 - 6) + .....+ (25 - 26)
= -1 + (-1) + ( -1 ) +...+ ( -1 ) {có 13 số )
= -13
b) tương tự nhé bn

Kết quả là 2870.
Giải nhanh bằng công thức tổng bình phương:
\(1^{2} + 2^{2} + \hdots + n^{2} = \frac{n \left(\right. n + 1 \left.\right) \left(\right. 2 n + 1 \left.\right)}{6}\)
Với \(n = 20\):
\(\frac{20 \cdot 21 \cdot 41}{6} = \frac{17220}{6} = 2870.\)
Ta có biểu thức:
\(1\times1+2\times2+3\times3+\ldots+20\times20=1^2+2^2+3^2+\ldots+20^2\)
Đây là tổng các số chính phương từ 1 đến 20.
Áp dụng công thức tổng bình phương:
\(1^2+2^2+3^2+\ldots+n^2=\frac{n \left(\right. n + 1 \left.\right) \left(\right. 2 n + 1 \left.\right)}{6}\)
Thay \(n = 20\):
\(\frac{20 \times 21 \times 41}{6} = \frac{17220}{6} = 2870\)