Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O K a)Xét tứ giác OBKC, ta có:
OC//BK(BK//AC)
BO//KC(KC//BD)
=>tứ giác OBKC là hình bình hành
lại có:
AC \(\perp\) BD ( hai đường chéo)
BD//KC
=> \(\)góc OCK =90o
=> hình bình hành OBKC là hình chữ nhật
b)Ta có:
BC = OK ( do OCKD là hình chữ nhật)
AB=BC( cách cạnh hình thoi bằng nhau)
=> AB = OK
c)
* nếu tứ giác ABCD là hình vuông:
=>BD=AC
mà: BO=1/2BD
OC=1/2AC
=> BO = OC
=> hình chữ nhật OBKC là hình vuông.
Vậy HCN OBKC là hình vuông khi hình thoi ABCD là hình vuông

Bài 2:
Cách 1:
\(x^3-7x-6=x^3-3x^2+3x^2-9x+2x-6\)
\(=\left(x^3-3x^2\right)+\left(3x^2-9x\right)+\left(2x-6\right)\)
\(=x^2.\left(x-3\right)+3x.\left(x-3\right)+2.\left(x-3\right)\)
\(=\left(x-3\right).\left(x^2+3x+2\right)\)
\(=\left(x-3\right).\left(x^2+x+2x+2\right)\)
\(=\left(x-3\right).\left[\left(x^2+x\right)+\left(2x+2\right)\right]\)
\(=\left(x-3\right).\left[x.\left(x+1\right)+2.\left(x+1\right)\right]\)
\(=\left(x-3\right).\left(x+1\right).\left(x+2\right)\)
Cách 2:
\(x^3-7x-6=x^3+x^2-x^2-x-6x-6\)
\(=\left(x^3+x^2\right)-\left(x^2+x\right)-\left(6x+6\right)\)
\(=x^2.\left(x+1\right)-x.\left(x+1\right)-6.\left(x+1\right)\)
\(=\left(x+1\right).\left(x^2-x-6\right)\)
\(=\left(x+1\right).\left(x^2+2x-3x-6\right)\)
\(=\left(x+1\right).\left[\left(x^2+2x\right)-\left(3x+6\right)\right]\)
\(=\left(x+1\right).\left[x.\left(x+2\right)-3.\left(x+2\right)\right]\)
\(=\left(x+1\right).\left(x+2\right).\left(x-3\right)\)
Chúc bạn học tốt!!! Còn 1 cách nữa nhưng mình mỏi tay quá!!! ![]()
![]()
a, \(x^3-9x^2+6x+16=x^3+x^2-10x^2-10x+16x+16\)
\(=\left(x^3+x^2\right)-\left(10x^2+10x\right)+\left(16x+16\right)\)
\(=x^2.\left(x+1\right)-10x.\left(x+1\right)+16.\left(x+1\right)\)
\(=\left(x+1\right).\left(x^2-10x+16\right)\)
\(=\left(x+1\right).\left(x^2-2x-8x+16\right)\)
\(=\left(x+1\right).\left[\left(x^2-2x\right)-\left(8x-16\right)\right]\)
\(=\left(x+1\right).\left[x.\left(x-2\right)-8.\left(x-2\right)\right]\)
\(=\left(x+1\right).\left(x-2\right).\left(x-8\right)\)
Chúc bạn học tốt!!!

A B C D M N P Q K
Bạn cần thêm điều kiện AB = AD .
Gọi K là trung điểm của AD. Dễ dàng chứng minh được MNPQ là hình vuông
Suy ra : \(S_{MNPQ}=\frac{NQ^2}{2}\)
Mặt khác, ta luôn có : \(KQ+QN\ge KN\) \(\Rightarrow QN\ge\left|KN-KQ\right|=\frac{1}{2}\left|c-a\right|\)
\(\Rightarrow QN^2\ge\frac{\left(c-a\right)^2}{4}\Rightarrow S_{MNPQ}=\frac{QN^2}{2}\ge\frac{\left(c-a\right)^2}{8}\)
Dấu "=" xảy ra khi M , Q, N thẳng hàng => AB // CD
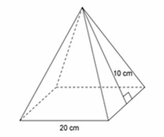

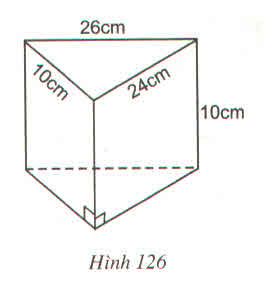

Đáp án cần chọn là: C