Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Cách 1: y' = (9 -2x)'(2x3- 9x2 +1) +(9 -2x)(2x3- 9x2 +1)' = -2(2x3- 9x2 +1) +(9 -2x)(6x2 -18x) = -16x3 +108x2 -162x -2.
Cách 2: y = -4x4 +36x3 -81x2 -2x +9, do đó
y' = -16x3 +108x2 -162x -2.
b) y' = .(7x -3) +
(7x -3)'=
(7x -3) +7
.
c) y' = (x -2)'√(x2 +1) + (x -2)(√x2 +1)' = √(x2 +1) + (x -2) = √(x2 +1) + (x -2)
= √(x2 +1) +
=
.
d) y' = 2tanx.(tanx)' - (x2)' =
.
e) y' = sin
=
sin
.
a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.
a) Ta có 
= 22 +2.2 +4 = 12.
Vì 
nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12
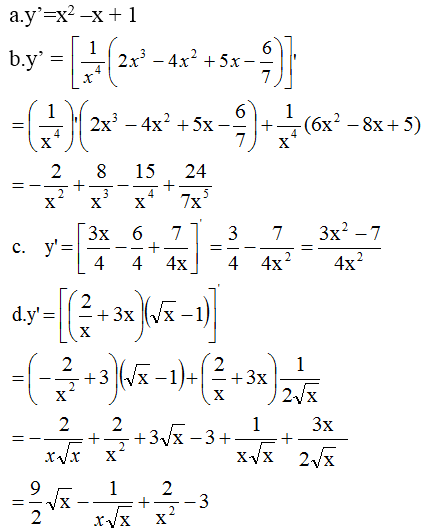
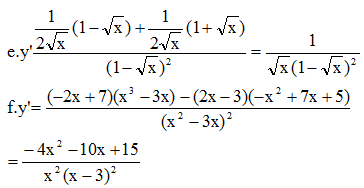
a.
\(y=\left\{{}\begin{matrix}x-2\left(x\ge2\right)\\2-x\left(x\le2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y'\left(2^+\right)=1\\y'\left(2^-\right)=-1\end{matrix}\right.\)
\(\Rightarrow y'\left(2^+\right)\ne y'\left(2^-\right)\Rightarrow\) không tồn tại đạo hàm tại \(x=2\)
b.
\(y=\left|x-2\right|^2=x^2-4x+4\Rightarrow y'=2x-4\)
\(\Rightarrow y'\left(2\right)=0\)
c.
\(y=\left\{{}\begin{matrix}4-x^2\left(\text{với }-2< x< 2\right)\\x^2-4\left(\text{với }x\ge2;x\le-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y'\left(2^+\right)=2x=4\\y'\left(2^-\right)=-2x=-4\end{matrix}\right.\)
\(\Rightarrow y'\left(2^+\right)\ne y'\left(2^-\right)\Rightarrow\) ko tồn tại đạo hàm tại \(x=2\)
d. Tương tự a và c