NR
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
6 tháng 1 2016
dien tich hinh thoi lon nhat khi do dai 2 duong cheo bang nhau (no chinh la hinh vuong)
4x4=16
TM
0
Y
2 tháng 9 2017
Bn ko có hình nên mik sẽ trả lời theo cảm tính,mong bn thông cảm nha:
Diện tích của các hình thoi nào có cạnh bằng a thì đều bằng nhau.Vì:
Hình thoi có bốn cạnh bằng nhau nên các hình thoi đó bằng nhau (theo tính chất hình thoi).
Vậy ko có hình thoi nào có diện tích lớn nhất vì các hình thoi đều bằng nhau.
CM
4 tháng 2 2017
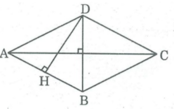
Giả sử có hình thoi ABCD. Kẻ DH ⊥ AB.
Ta có: S A B C D = AB.DH
Tam giác AHD vuông tại H nên: DH ≤ AD
Mà AB = AD (gt)
Nên: S A B C D ≤ A B 2
Vậy S A B C D có giá trị lớn nhất bằng A B 2
Khi đó ABCD là hình vuông.
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.
2 tháng 1 2020
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)
6 tháng 1 2024
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
CM
23 tháng 2 2017
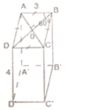
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
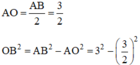
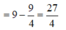
x y A B D C O
Giả sử hình thoi đó là ABCD , hai đường chéo cắt nhau tại O.
Đặt OA = x (x>0) (cm) , OD = y (y>0) (cm)
Ta có : \(x^2+y^2=16\)
Mặt khác : \(AC=2x,BD=2y\Rightarrow S_{ABCD}=\frac{1}{2}\times AC\times BD=\frac{1}{2}\times2x\times2y=2xy\)
Ta có bđt : \(x^2+y^2\ge2xy\Rightarrow2xy\le16\)
Vậy \(MAX_{S_{ABCD}}=16\) \(\Leftrightarrow\begin{cases}x=y\\x^2+y^2=16\end{cases}\) \(\Leftrightarrow x=y=2\sqrt{2}\) (cm)
Do cạnh của hình thoi là 4 cm
=> Hai đường chèo có độ dài là : 4.2 = 8 (cm)
Vậy Smax = (8.8) : 2 = 31 (cm2)