NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
1
5 tháng 3 2015
Ta có: x2-2y2=1
x2-1=2y2(x-1)(x+1)=2y2
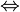x2-1=2y2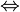(x-1)(x+1)=2y2vì 2y2\( {\vdots}\)2 nên (x-1)(x+1)\( {\vdots}\)2
vì x-1+x+1=2x 
x-1 và x+1 có cùng tính chẵn lẻ
(x-1)(x+1) là hai số chẵn liên tiếp
(x-1)(x+1)\( {\vdots}\)4 2y2\( {\vdots}\)4 y2\( {\vdots}\)2 y\( {\vdots}\)2 y = 2
Và từ y=2 ta thay vào x2-2y2=1 x2-2.22=1 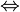x2 = 9 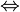x = 3
Vật số nguyên tố (x, y) là cặp số (3, 2)
HT
0
AT
0
HT
0
15 tháng 1 2020
d. Câu hỏi của Black - Toán lớp 7 - Học toán với OnlineMath
1 tháng 3 2016
Biến đổi bt tương đương : (x^2-1)/2 =y^2
Ta có: vì x,y là số nguyên dương nên
+) x>y và x phải là số lẽ.
Từ đó đặt x=2k+1 (k nguyên dương);
Biểu thức tương đương 2*k*(k+1)=y^2 (*);
Để ý rằng:
Y là 1 số nguyên tố nên y^2 sẽ là 1 số nguyên dương mà nó có duy nhất 3 ước là :
{1,y, y^2} ;
từ (*) dễ thấy y^2 chia hết cho 2, dĩ nhiên y^2 không thể là 2, vậy chỉ có thể y=2 =>k=1;
=>x=3.
Vậy ta chỉ tìm được 1 cặp số nguyên tố thoả mãn bài ra là x=3 và y=2 (thoả mãn).
S
1
N
1
G
8 tháng 3 2019
\(f\left(x\right)=ax^2+bx+c\Rightarrow\hept{\begin{cases}f\left(0\right)=c\\f\left(1\right)=a+b+c\\f\left(2\right)=4a+2b+c\end{cases}}\)
\(f\left(0\right)\) nguyên \(\Rightarrow c\) nguyên \(\Rightarrow\hept{\begin{cases}2a+2b\\4a+2b\end{cases}}\) nguyên
\(\Rightarrow\left(4a+2b\right)-\left(2a+2b\right)=2a\)(nguyên)
\(\Rightarrow2b\) nguyên
\(\Rightarrowđpcm\)
y = 2 , x = -3
y = 2 , x =3
y = -2 , x = -3
y = - 2 , x =3