Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)

Ta có : \(y'=4x^3-4\left(m-1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m-1\right)x=0\Leftrightarrow x\left[x^2-\left(m-1\right)\right]=0\)
Trường hợp 1 : nếu \(m-1\le0\Leftrightarrow m\le1\), hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\), vậy \(m\le1\) thỏa mãn yêu cầu bài toán
Trường hợp 2 : nếu \(m-1>0\Leftrightarrow m>1\), hàm số đồng biến trên khoảng \(\left(-\sqrt{m-1};0\right)\) và \(\left(\sqrt{m-1};+\infty\right)\)
Để hàm số đồng biến trên khoảng (1;3) thì \(\left(\sqrt{m-1}\le1\Leftrightarrow m\le2\right)\)
Vậy hàm số đồng biến trên khoảng (1;3) \(\Leftrightarrow m\in\left(-\infty;2\right)\)

Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
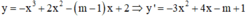
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
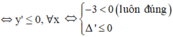
![]()
![]()
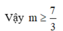

y'=2x2-2(2m-3)x+2(m2-3m)=2(x-m)(x-m+3) => h/s nghịch biến trên (m-3; m) => YCBT <=> m-3 =<1 và 3=<m <=> 3=<m=<4

Chọn D.
Tập xác định: D = ℝ
Ta có ![]()
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
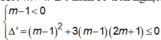
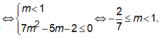
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.


y
′
=g(x)=3x
2
−2(m+1)x−(2m
2
−3m+2)
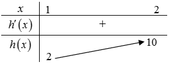
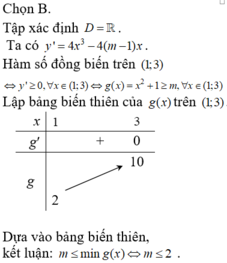
Để hàm số đồng biến trên khoảng đã cho
⇔
𝑔
(
𝑥
)
≥
0
;
∀
𝑥
≥
2
⇔g(x)≥0;∀x≥2
Δ
′
=
(
𝑚
+
1
)
2
+
3
(
2
𝑚
2
−
3
𝑚
+
2
)
=
7
(
𝑚
−
1
2
)
2
+
21
4
>
0
;
∀
𝑚
Δ
′
=(m+1)
2
+3(2m
2
−3m+2)=7(m−
2
1
)
2
+
4
21
>0;∀m
⇒
⇒ Để
𝑔
(
𝑥
)
≥
0
;
∀
𝑥
≥
2
⇔
𝑥
1
<
𝑥
2
≤
2
g(x)≥0;∀x≥2⇔x
1
<x
2
≤2
⇔
{
(
𝑥
1
−
2
)
(
𝑥
2
−
2
)
≥
0
𝑥
1
+
𝑥
2
2
<
2
⇔{
(x
1
−2)(x
2
−2)≥0
2
x
1
+x
2
<2
⇔
{
𝑥
1
𝑥
2
−
2
(
𝑥
1
+
𝑥
2
)
+
4
≥
0
𝑥
1
+
𝑥
2
<
4
⇔{
x
1
x
2
−2(x
1
+x
2
)+4≥0
x
1
+x
2
<4
⇔
{
−
1
3
(
2
𝑚
2
−
3
𝑚
+
2
)
−
4
3
(
𝑚
+
1
)
+
4
≥
0
2
3
(
𝑚
+
1
)
<
4
⇔{
−
3
1
(2m
2
−3m+2)−
3
4
(m+1)+4≥0
3
2
(m+1)<4
⇔
{
−
2
𝑚
2
−
𝑚
+
6
≥
0
2
𝑚
<
10
⇔{
−2m
2
−m+6≥0
2m<10
⇒
−
2
≤
𝑚
≤
3
2
⇒−2≤m≤
2
3