Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

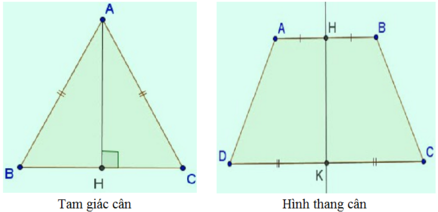
- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).
– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.

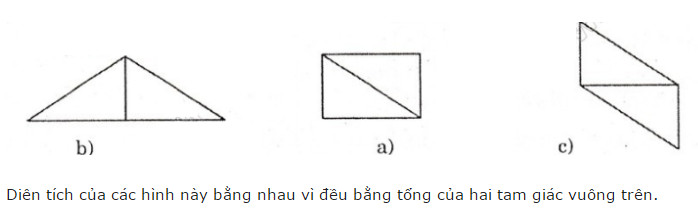
Ta ghép như sau:
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.

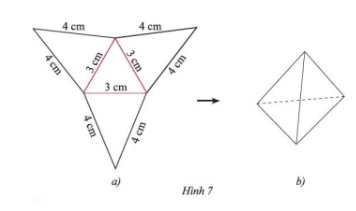
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.

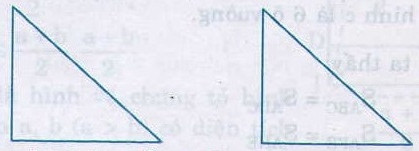
Cắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
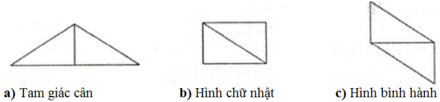
Ghép hai tam giác trên để tạo thành:

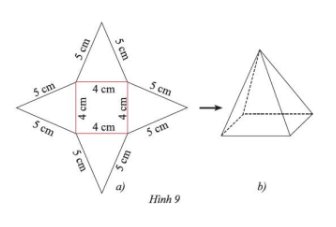
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Chú ý:
- ∆ABC cân tại A có trục đối xứng là đường phân giác của góc BAC.
- Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng.
Đối với tam giác cân hình 38a:
Đối với tam giác cân hình 38a:
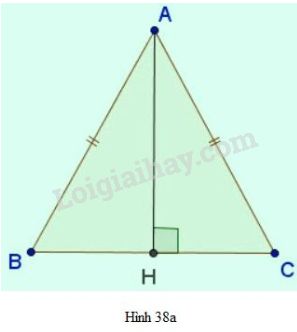
∆ABC cân tại A , trục đối xứng là đường cao AH với H là trung điểm của đoạn BC. - Đối với hình thang cân hình 38b:Hình thang cân ABCD (AB // CD), trục đối xứng là đường thẳng KH với K, H lần lượt là trung điểm của AB và CD.