Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
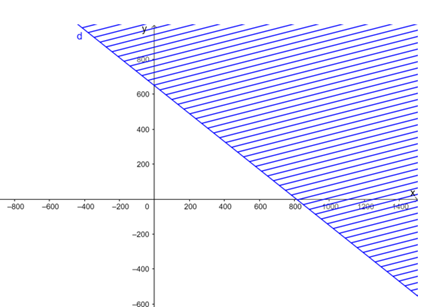
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
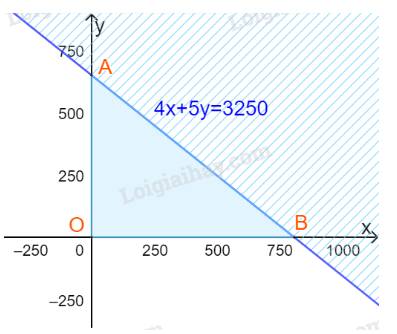
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.

Giải:
Gọi số tiền ông Sáu gửi ban đầu là x.
Theo đề bài ta có:
Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)
Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)
Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)
Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)
Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng
Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.
Tổng % lãi suất trong 2 năm là :
6% . 2 = 12%
Số tiền lãi trong 2 năm là :
112360000 . 12% = 13483200
=> Tiền ông Sáu gửi là :
112360000 - 13483200 = 98876800

a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)
\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)
\(=14\)
a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1

hahaha
nghe mà bật cười thế nhở
thiệt sự rất buồn cười luôn
# câu trả lwoif chỉ mang tính chất hài hước
mong olm k trừ điểm

Đáp án: C
Ta có một năm có 365 ngày, một ngày có 24 giờ, một giờ có 60 phút và một phút có 60 giây.
Vậy một năm có 24.365.60.60 = 31536000 giây.
Vì vận tốc ánh sáng là 300 nghìn km/s nên trong vòng một năm nó đi được 31536000.300 = 9,4608.109 km.
0 km vì 1 vật có khối lượng ko thể đạt tới vận tốc ánh sáng, và chắc chắc ko có nhà khoa học nào lại nghiên cứu 1 máy bay vs tốc độ 7 lần vận tốc ánh sáng