Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: điều kiện xác định của bpt \(x+3-\dfrac{1}{x+7}< -\dfrac{1}{x+7}\) là \(x\ne-7\)
\(\Rightarrow x=-7\) không phải là nghiệm của bpt trên
Lại có: \(x+3< 2\\ \Leftrightarrow x< 2-3\\ \Leftrightarrow x< -1\)
\(\Rightarrow x=-7\) thỏa mãn bpt \(x+3< 2\) \(\left(-7< -1\right)\)

TXĐ:D=R\{-2;1}
BPT<=>\(\dfrac{\left(x-1\right)^2-\left(x+2\right)^2}{\left(x-1\right)\left(x+2\right)}\ge0\)
<=>\(\dfrac{-3\left(2x+1\right)}{\left(x-1\right)\left(x+2\right)}\ge0\)
Cho 2x+1=0<=>x=-0,5
cho (x-1)(x+2)=0 <=>x=1 hoặc x=-2
Bảng xét dấu:
x -\(\infty\) -2 -0,5 1 +\(\infty\)
f(x) + kxđ - 0 + kxđ -
=>Tập nghiệm T=(-\(\infty\);-2)\(\cup\)[-0,5;1]

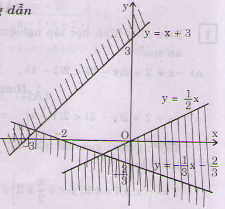
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
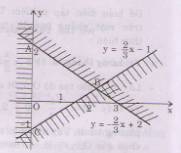
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).

a) Ta có: \(x^2+\dfrac{1}{x^2+1}=x^2+1+\dfrac{1}{x^2+1}-1\)\(\ge2\sqrt{\left(x^2+1\right).\dfrac{1}{x^2+1}}-1=2-1=1\).
Vì vậy: \(x^2+\dfrac{1}{x^2+1}\ge1\) nên BPT vô nghiệm.
b) Áp dụng BĐT Cô-si ta có:
\(\sqrt{x^2-x+1}+\dfrac{1}{\sqrt{x^2-x+1}}\ge\)\(2\sqrt{\left(x^2-x+1\right).\dfrac{1}{x^2-x+1}}=2\).
Vì vậy BPT vô nghiệm.

1 ) \(|\) x+2 \(|\) - \(|\) x-1 \(|\) < x - 3/2
TH1 : x < -2
bpt <=> -x - 2 - ( -x + 1) < x - 3/2
<=> x > -3/2 ( k tm )
TH 2 : -2 \(\le\) x < 1
bpt <=> x + 2 - ( -x+1) < x - 3/2
<=> x < -5/2 (k tm )
TH3 : x \(\ge\) 1
bpt <=> x + 2 - ( x - 1 ) < x - 3/2
<=> x > 9/2 tm
Vậy x > 9/2 .
2 ) x(x - 1)2 \(\ge\) 4 - x
<=> x( x2 - 2x +1 + 1 ) \(\ge\) 4
<=> x3 - 2x2 + 2x - 4 \(\ge\) 0
<=> x2 (x - 2) + 2(x - 2) \(\ge\) 0
<=> (x2 + 2)(x - 2) \(\ge\) 0
Có : x2 + 2 > 0 , với mọi x
=> x - 2 \(\ge\) 0 <=> x \(\ge\) 2 .
Xem thử đúng hay sai ...
Hoàng Thị Ánh Phương , Ribi Nkok Ngok, Nguyễn Lê Phước Thịnh, Trần Quốc Khanh, Vũ Minh Tuấn, ?Amanda?, Nguyễn Ngọc Lộc , Trên con đường thành công không có dấu chân của kẻ lười biếng, Bùi Lan Anh , Akai Haruma, @Nguyễn Việt Lâm, ...

a) Đkxđ: \(x\ne1,x\ne0\)
⇔x+1x−1+2>x−1x⇔2x−1+2>−1x⇔x+1x−1+2>x−1x⇔2x−1+2>−1x
⇔2x−1+1x+2>0⇔2x+x−1+2(x2−x)(x−1)x=2x2+x−1(x−1)(x)>0⇔2x−1+1x+2>0⇔2x+x−1+2(x2−x)(x−1)x=2x2+x−1(x−1)(x)>0
Tử {delta =9}
−1<x<12⇒T

Cái này nãy tui mới làm ở bên h_ọ_c_24 ý.
\(x\left(x-1\right)^2\ge4-x\)
\(\Leftrightarrow x\left(x^2-2x+1\right)\ge4-x\)
\(\Leftrightarrow x^3-2x^2+x\ge4-x\)
\(\Leftrightarrow x^3-2x^2+2x-4\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2\right)\ge0\)
\(\Leftrightarrow x-2\ge0\left(Vì:x^2+2>0\forall x\right)\)
\(\Leftrightarrow x\ge2\)
Vậy \(S=\left\{2;+\infty\right\}\)
@ Băng Băng @ Mình không kí hiệu tập nghiệm như vậy nhé em:
S = [ 2; \(+\infty\))
Bạn xem lại đề, đề thiếu dữ kiện để thành bất phương trình.