Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

bạn để ý có công thức T= \(mg\left(3cos\alpha-2cos\alpha_0\right)\)
còn P= mg
vậy T/P= \(3cos\alpha-2cos\alpha_0\)
a0* l = S0 bạn suy ra a0 ( l: chiều dài con lắc ; w2 = g/l)
chú ý: con lắc qua vị trí cân bằng tức \(\alpha=0\) suy ra cos \(\alpha\) = 1
suy ra T/P cần tìm = 3 - 2cos\(\alpha_0\)
bạn hiểu rồi thì tính nốt nhé
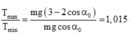
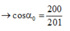

 =2 7,1 cm/s
=2 7,1 cm/s
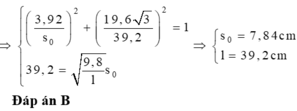
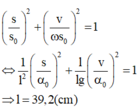
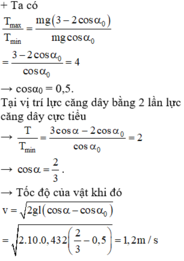
Đáp án C