
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

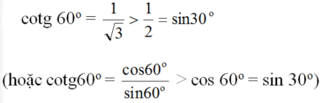


c) \(cotg44^0.cotg45^0.cotg46^0=cotg45^0=1\)
(vì \(cotg44^0=tg46^0\) (do \(44^0+46^0=90^0\) )
mà \(tg46^0.cot46^0=1\) )

Ta có B = sin245o + sin262o + sin227o - (sin247o = sin248o)
sin227o = cos263o
mà cos263o < cos262o
=> sin262o + cos263o < sin262o + cos262o
hay sin262o + sin227o <1 (1)
sin248o = cos242o
mà cos242o > cos247o
=> sin247o + cos242o > sin247o + cos247o
hay sin247o + sin248o > 1
=> - (sin247o + sin248o) <1 (2)
Từ (1) và (2) ta thấy:
sin262o + sin227o - (sin247o = sin248o) < 1
sin245o = 1/2 <1
=> B = sin245o + sin262o + sin227o - (sin247o = sin248o) <1
=> B < A
cái chỗ (sin247o = sin248o) thay thành (sin247o + sin248o) nha ^_^

a) Ta có: sin30=cos60, sin50=cos40
Mà cos30 < cos38 < cos40 < cos60 < cos80
Nên cos30 < cos38 < sin50 < sin30 < cos80
b) Ta có: tan75=cot15, tan63=cot27 => cot11 < tan75 < cot20 < tan63 (1)
và: sin49=cos41 => cos30 < sin49 (2)
Lại có: cot11=tan69 > tan49= sin49:cos49 > sin49 (do cos49<1) (3)
Từ (1), (2) và (3) suy ra: cos30 < sin49 < cot11 < tan75 < cot20 < tan63
TA CÓ \(\sin30\)= \(\cos60\)
\(\sin50=\cos40\)
---->> \(\cos30< \cos38< \cos40< \cos60< \cos80\)
------>> \(\cos30< \cos38< \sin50< \sin60< \cos80\)
Cái kia làm tương tự nhoa
Bạn xin 1 cái k

a, \(\cos^215+\cos^225+\cos^235+\cos^245+\sin^235+\sin^225+\sin^215\)
=\(\left(\cos^215+\sin^215\right)+\left(\cos^225+\sin^225\right)+\left(\cos^235+\sin^235\right)+\cos^245\)
=\(1+1+1+\frac{1}{2}=\frac{7}{2}\)
b.\(\sin^210-\sin^220-\sin^230-\sin^240-\cos^240-\cos^220+\cos^210\)
=\(\left(\sin^210+\cos^210\right)-\left(\sin^220+\cos^220\right)-\left(\sin^240+\cos^240\right)-\sin^230\)
=\(1-1-1-\frac{1}{4}=-\frac{5}{4}\)
c,\(\sin15+\sin75-\sin75-\cos15+\sin30=\sin30=\frac{1}{2}\)

sin20<sin70
cos25 > cos65*15'
tan73*20' >tan45
cotg2 >cotg73*40'
tan25>sin25
cotg32 >cos32