Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a)Ta có:
C=1957/2007=1957+50-50/2007
=2007-50/2007
=2007/2007-50/2007
=1-50/2007
D=1935/1985=1935+50-50/1985
=1985-50/1985
=1985/1985-50/1985
=1-50/1985
Vì 50/2007<50/1985 nên -50/2007>-50/1985
⇒C>D
b)Ta có:
A=20162016+2/20162016-1
A=20162016-1+3/20162016-1
A=20162016-1/20162016-1+3/20162016-1
A=1+3/20162016-1
Tương tự: B=20162016/20162016-3
B=1+3/20162016-3
Vì 20162016-1>20162016-3 nên 3/20162016-1<3/20162016-3
⇒A<B
Chúc bạn học tốt!
Làm tiếp:
c)Ta có:
M=102018+1/102019+1
10M=10.(102018+1)/202019+1
10M=102019+10/102019+1
10M=102019+1+9/102019+1
10M=102019+1/102019+1 + 9/102019+1
10M=1+9/102019+1
Tương tự:
N=102019+1/102020+1
10N=1+9/102020+1
Vì 9/102019+1>9/102020+1 nên 10M>10N
⇒M>N
Chúc bạn học tốt!

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.

Còn một cái nữa là ta có thể so sánh với số trung gian như 1 và 0 .
Vì a/b=c/d khi a.c=b.d
Giờ thì mình kết thúc bài làm.

Theo quy ước với mọi phân số lớn hơn 0 thì ta có:
\(\dfrac{a}{b}>0=>\dfrac{a}{b}< \dfrac{a+n}{b+n}\left(n\in N;n\ne0\right)\)
Áp dụng với bài trên ta => ĐPCM
CHÚC BẠN HỌC TỐT.......

\(a,\frac{20132013}{20142014}=\frac{2013.10001}{2014.10001}=\frac{2013}{2014}=1-\frac{1}{2014};\frac{131313}{141414}=\frac{13.10101}{14.10101}=\frac{13}{14}=1-\frac{1}{14}.\text{Vì: 14 bé hơn 2014 nên:}\frac{1}{14}>\frac{1}{2014}\Rightarrow\frac{20132013}{20142014}>\frac{131313}{141414}\)
\(C=2013^9+2013^9.2013=2013^9\left(2013+1\right)=2013^9.2014;D=2014^9.2014\text{ vì: 2013^9< 2014^9 nên: C bé thua D }\)
\(c,M=\frac{-7}{10^{2005}}+\frac{-15}{10^{2006}}=\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}+\frac{-8}{10^{2006}};N=\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}+\frac{-8}{10^{2005}}.Vì:10^{2006}>10^{2005}.Nên:\frac{-8}{10^{2006}}>\frac{-8}{10^{2005}}\Rightarrow M>N\)

a) \(\frac{6}{7}\) và \(\frac{11}{10}\)
\(\frac{6}{7}< 1\)
\(\frac{11}{10}>1\)
\(\Rightarrow\frac{6}{7}< 1< \frac{11}{10}\Rightarrow\frac{6}{7}< \frac{11}{10}\)
b) \(\frac{-5}{17}\) và \(\frac{2}{7}\)
\(\frac{-5}{17}< 0\)
\(\frac{2}{7}>0\)
\(\Rightarrow\frac{-5}{17}< 0< \frac{2}{7}\)\(\Rightarrow\frac{-5}{17}< \frac{2}{7}\)
c) \(\frac{419}{-723}\) và \(\frac{-697}{-313}\)
\(\frac{419}{-724}< 0\)
\(\frac{-697}{-313}>0\)
\(\Rightarrow\frac{419}{-724}< 0< \frac{-697}{-313}\Rightarrow\frac{419}{-723}< \frac{-697}{-313}\)

a) \(\left\{{}\begin{matrix}\dfrac{11}{10}>\dfrac{10}{10}\\\dfrac{10}{10}=\dfrac{7}{7}>\dfrac{6}{7}\end{matrix}\right.\) \(\Rightarrow\dfrac{11}{10}>\dfrac{6}{7}\)
b) \(\left\{{}\begin{matrix}\dfrac{2}{7}>\dfrac{0}{7}\\\dfrac{0}{7}=\dfrac{0}{17}>-\dfrac{5}{17}\end{matrix}\right.\) \(\Rightarrow\dfrac{2}{7}>\dfrac{-5}{17}\)
c)
\(\left\{{}\begin{matrix}\dfrac{-697}{-313}=\dfrac{697}{313}>\dfrac{0}{313}\\\dfrac{0}{313}=\dfrac{0}{723}>\dfrac{-419}{723}=\dfrac{419}{-723}\end{matrix}\right.\) \(\Rightarrow\dfrac{-697}{-313}>\dfrac{419}{-723}\)
Mk chỉ cho gợi ý thôi nha.
Cũng không khó lắm nên bạn có thể tự làm mà.
a) So sánh với 1
b) So sánh với 0
c) So sánh với 0
Chúc bạn học tốt!

a: 51/56=1-5/56
61/66=1-5/66
mà -5/56<-5/66
nên 51/56<61/66
b: 41/43<1<172/165
c: \(\dfrac{101}{506}>0>-\dfrac{707}{3534}\)
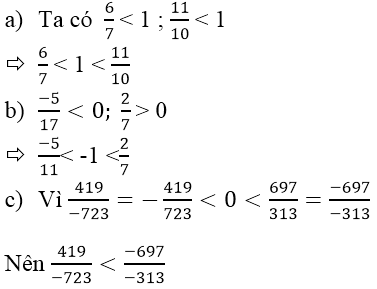
\(C=\dfrac{1957}{2007}\) và \(D=\dfrac{1935}{1985}\)
\(\Rightarrow\left\{{}\begin{matrix}C=\dfrac{1957}{2007}\\D=\dfrac{1935}{1985}\end{matrix}\right.\\\Rightarrow\left\{{}\begin{matrix}C=1-\dfrac{50}{2007}\\D=1-\dfrac{50}{1985}\end{matrix}\right. \)
Vì \(\dfrac{50}{2007}<\dfrac{50}{1985}\)
\(\Rightarrow1-\dfrac{50}{2007}>1-\dfrac{50}{1985}\\\Rightarrow C>D\)