K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0

NN
0

TP
14

QT
Quoc Tran Anh Le
Giáo viên
2 tháng 11 2023
a)
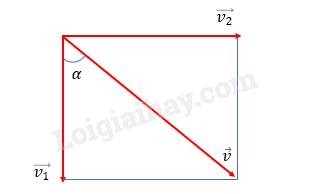
b) Ta có: v = 24 (m/s); v1 = 17 m/s
Từ sơ đồ, ta có: \({v^2} = v_1^2 + v_2^2\) (theo định lí Pytago trong 1 tam giác vuông)
=> \({v_2} = \sqrt {{v^2} - v_1^2} = \sqrt {{{24}^2} - {{17}^2}} \approx 16,94(m/s)\)
c) Gọi góc hợp bởi \(\overrightarrow v \) và \(\overrightarrow {{v_1}} \) là \(\alpha \)
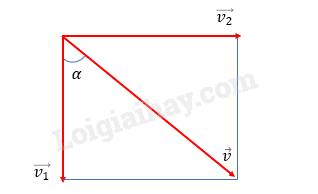
Góc giữa vận tốc của viên đá và phương thẳng đứng khi nó chạm vào mặt nước là:
\(\cos \alpha = \frac{{{v_1}}}{v} = \frac{{17}}{{24}} \Rightarrow \alpha \approx {44^0}54'\)