Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

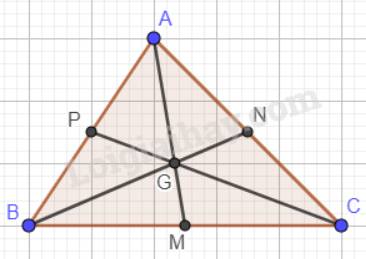
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).

- Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.
Do đó, AM có là đường trung tuyến của tam giác ABC
- Ta có:
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)

Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.

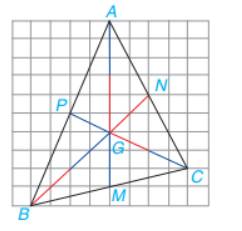
Vì G là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\)
Ta có: \(GN = BN – BG = BN - \dfrac{2}{3}BN = \dfrac{1}{3}BN;\\ GP = CP – CG = CP - \dfrac{2}{3}CP = \dfrac{1}{3}CP\)
Do đó, \(BN = 3. GN ; CP = 3. GP\)
Như vậy, \(BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN;\\CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP\)
Vậy \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\);
\(BG = 2GN; CG = 2GP\).

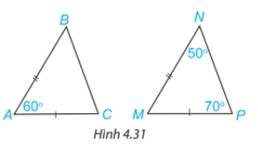
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Bài làm
Ta có: \(AG=\frac{2}{3}AM\)
\(CG=\frac{2}{3}CP\)
\(BG=\frac{2}{3}BN\)
Mà AG = BG = CG
=> \(\frac{2}{3}AM=\frac{2}{3}CP=\frac{2}{3}BN\)
=> \(AM=CP=BN\)
Vì AG = GC ( gt )
=> Tam giác AGC cân tại G
Mà BN là đường trung tuyến và G thuộc BN
=> GN cũng là đường trung tuyến
=> GN là đường cao ( do tam giác AGC cân ở G )
=> Tam giác ABC cân ở B
=> AB = BC (1)
Vì AG = GB ( gt )
=> Tam goác AGB cân tại G
Mà CP là đường trung tuyến và G thuộc CP
=> GN là đường trung tuyến
Và GN cũng là đường trung tuyến của tam giác cân AGC
=> GN cũng là đường cao
=> CP cũng là đường cao.
=> Tam giác ACB cân ở C
=> AC = BC (2)
Vì BG = GC ( gt )
=> Tam giác BGC cân tại G
Mà AM là đường trung tuyến và G thuộc AM
=> GM cũng là đường trung tuyến của tam giác GBC
Và GM là đường cao
=> AM cũng là đường cao
=> Tam giác ABC cân ở A
=> AB = AC (3)
Từ (1) và (2) và (3) => AB = AC = BC
=> Tam giác ABC đều.
# Học tốt #
A B C N P M G
Ta có: AG = GB (gt) => t/giác AGB cân tại G có GN là đường trung tuyến
=> GN cũng là đường cao của t/giác AGB
Hay CN là đường cao của t/giác ABC (Do C, G, N | | | )
mà CN cũng là đường trung tuyến
=> t/giác ACB cân tại C => AC = CB (1)
BG = GC (gt) => t/giác BGC cân tại G có GM là đường trung tuyến
=> GM cũng là đường cao của t/giác GBC
hay AM là đường cao của t/giác ABC (Do A; G; M | | | )
mà AM cũng là đường trung tuyến của t/giác ABC
=> t/giác ABC cân tại A => AB = AC (2)
Từ (1) và (2) => AB = AC = BC
=> t/giác ABC đều
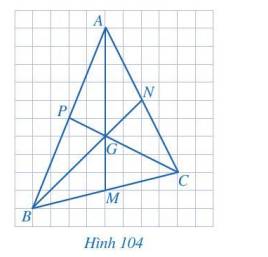

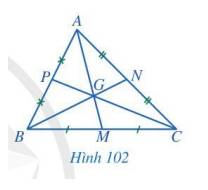

Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).