Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kiến thức áp dụng
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

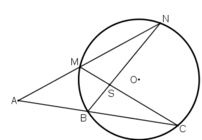

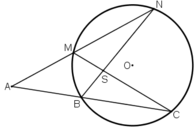
⇒ A ^ + B S M ^
= 1 2 . s đ N C ⏜ - s đ B M ⏜ + 1 2 s đ N C ⏜ + s đ M B ⏜ = s đ N C ⏜ 1
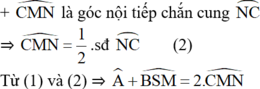
(đpcm)

a: góc OIA+góc OCA=180 độ
=>OIAC nội tiếp
b: Gọi giao của DC và OA là H
=>BC vuông góc OA tại H
Xét ΔOHD vuông tại H và ΔOIA vuông tại I có
góc HOD chung
=>ΔOHD đồng dạng với ΔOIA
=>OH*OA=OI*OD
=>OI*OD=R^2

a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: góc OHM=góc ONM=90 độ
=>OHNM nội tiếp
=>góc MON=góc MHN

1: góc CHO+góc CNO=180 độ
=>CHON nội tiếp
2: Xét ΔKON và ΔKCH có
góc KON=góc KCH
góc K chung
=>ΔKON đồng dạng với ΔKCH
=>KO/KC=KN/KH
=>KO*KH=KN*KC

a)
ta có SA= SB(t/c tiếp tuyến cắt nhau)
nên tam giác SAB cân ở S
do đó SO vừa là phân giác vừa là đường cao nên SO vuông góc AB
I là trung điểm của MN nên OI vuông góc MN
do đó góc SHE=SIE = 90 độ
hai điểm H và I cùng nhìn đoạn SE dưới 1 góc vuông nên tứ giác IHSE nội tiếp
b) SOI đồng dạng với EOH vì có O chung
$\widehat{SHE}=\widehat{SIE}$ =90 độ chứng minh trên
suy ra $\dfrac{OI}{OH}$ = $\dfrac{OS}{OE}$
mà OH.OS = OB^2 = R^2(hệ thức lượng trong tam giác vuông SOB
nên OI.OE=R^2 (DPCM)