K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8
a: \(255=5\cdot51=5\cdot3\cdot17\)
b: \(630=63\cdot10=3^2\cdot7\cdot2\cdot5\)
HM
6
15 tháng 10 2017
Giải:
Ta phân tích số 2100:
\(2100=23.3.7.52\)
=>Số 2100 chia hết cho các số nguyên tố \(2;3;5;7\)
VK
6 tháng 6 2018
Vì \(2100=2^2.3.5^5.7\)
nên 2100 chia hết các thừa số nguyên tố là 2;3;5;7
DD
Đoàn Đức Hà
Giáo viên
17 tháng 10 2021
Ta có công thức: \(ab=\left(a,b\right).\left[a,b\right]\).
Áp dụng ta được:
Có \(120.200=24000\), \(BCNN\left(120,200\right)=600\)
suy ra \(ƯCLN\left(120,200\right)=\frac{24000}{600}=40\).
14 tháng 11 2014
Ta có:
312= 23 x 3 x 13
Vậy thừa số nguyên tố nhỏ nhất trong phân tích 312 thành tích các thừa số nguyên tố là 2
KD
29 tháng 7 2016
312= 23 x 3 x 13
Vậy thừa số nguyên tố nhỏ nhất trong phân tích 312 thành tích các thừa số nguyên tố là 2
13 tháng 10 2021
A) 160 = 2^5 x 5
220 = 2² x 5 x 11
120 = 2³ x 5 x 3
150 = 2 x 3 x 5²
LV
0
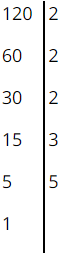
a: \(255=5\cdot51=5\cdot3\cdot17\)
b: \(630=63\cdot10=3^2\cdot7\cdot2\cdot5\)
c,ơn ạ