Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng có u1 = 1; d = 1
Giả sử có n hàng cây thì
Ta có 3003 = Sn = nu1 + ![]() ⇔ n2 + n – 6006 = 0 ⇔ n = 77.
⇔ n2 + n – 6006 = 0 ⇔ n = 77.

Chọn B.
Gọi số hàng cây là n.
Gọi số cây lần lượt trên các hàng là 1; 2; 3..; n.
Đây là một cấp số cộng với số hạng đầu u1 = 1; d = 1 .
Ta có:
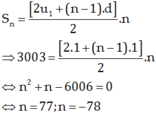
Vậy số hàng cần tìm là 77.

Theo đề bài ta có dãy số chỉ số ghế có ở các hàng là một cấp số cộng có số hạng đầu \({u_1} = 17\) và công sai \(d = 3\).
a) Số ghế có ở hàng cuối cùng là: \({u_{20}} = {u_1} + 19{\rm{d}} = 17 + 19.3 = 74\) (ghế).
b) Tổng số ghế có trong rạp là: \({S_{20}} = \frac{{20\left[ {2{u_1} + 19{\rm{d}}} \right]}}{2} = \frac{{20\left[ {2.17 + 19.3} \right]}}{2} = 910\) (ghế).

Ta có: \({u_1} = 15,\;d = 3\)
\({S_n} = \frac{n}{2}\left[ {2 \times 15 + \left( {n - 1} \right) \times 3} \right] = 870\)
\(\frac{n}{2}\left( {27 + 3n} \right) = 870\)
\(\begin{array}{l} \Leftrightarrow 3{n^2} + 27n - 1740 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 20\\n = - 29(L)\end{array} \right.\end{array}\)
Vậy cần phải thiết kế 20 hàng ghế.

Đáp án D.
Chọn 2 cây trong 6 cây xoài có C 6 2 = 15 cách.
Chọn 2 cây trong 4 cây mít có C 4 2 = 6 cách.
Chọn 2 cây trong 2 cây xoài có C 2 2 = 1 cách.
Suy ra có tất cả 15 . 6 . 1 = 90 cách chọn 6 cây trồng.
Vậy xác suất cần tính là
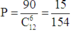

a) Ta có:
\(\begin{array}{l}{u_1} = 25\\{u_2} = 24 = {u_1} - 1\\{u_3} = 23 = {u_2} - 1\\ \vdots \end{array}\)
Vậy công thức truy hồi: \({u_n} = {u_{n - 1}} - 1\left( {n \ge 2} \right) \Leftrightarrow {u_n} - {u_{n - 1}} = - 1 < 0\).
Vậy \(\left( {{u_n}} \right)\) là dãy số giảm.
b) Ta có:
\(\begin{array}{l}{v_1} = 14\\{v_2} = 15 = {v_1} + 1\\{v_3} = 16 = {v_2} + 1\\ \vdots \end{array}\)
Vậy công thức truy hồi: \({v_n} = {v_{n - 1}} + 1\left( {n \ge 2} \right) \Leftrightarrow {v_n} - {v_{n - 1}} = 1 > 0\).
Vậy \(\left( {{v_n}} \right)\) là dãy số tăng.



Giải sữ người ta đã trồng được n hàng.
Số cây ở mỗi hàng lập thành một cấp số cộng với u1 = 1, công sai d = 1
Tổng số cây ở n hàng cây là:
\({S_n} = \frac{{n\left( {1 + n} \right)}}{2} = \frac{{n\left( {n + 1} \right)}}{2} = 4950\)
⇔ n2 + n – 9 900 = 0
⇔ n = 99 (thỏa mãn) hoặc n = – 100 (không thỏa mãn)
Vậy có 99 hàng cây được trồng theo cách trên.