Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

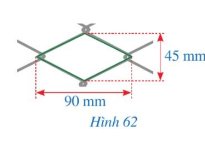
Giả sử mắt lưới cần tính độ dài cạnh là hình thoi ABCD.
Có. AC = 45mm; BD = 90mm.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên
\(\begin{array}{l}OA = OC = \dfrac{{AC}}{2} = \dfrac{{45}}{2} = 22,5(mm)\\OB = OD = \dfrac{{BD}}{2} = \dfrac{{90}}{2} = 45(mm)\end{array}\)
Xét \(\Delta AOB\) vuông tại O có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\{(22,5)^2} + {(45)^2} = A{B^2} \Rightarrow A{B^2} = 2.531,25 \Rightarrow AB \approx 50(mm)\end{array}\)

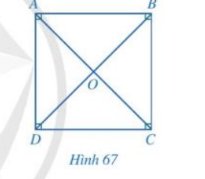
Do tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)

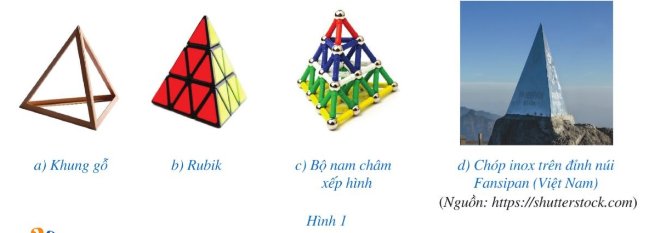
Những hình khối có dạng ở hình 11 được gọi là hình chóp tứ giác đều.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

Những hình khối có dạng như ở Hình 1 thường được gọi là hình chóp tam giác đều.

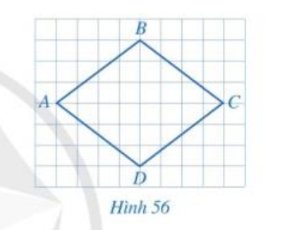
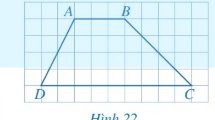
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

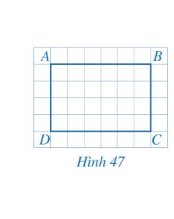
Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
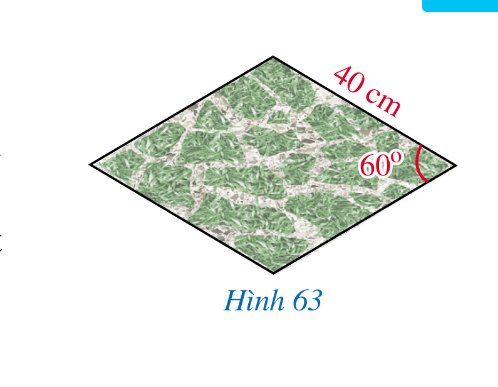







Giả sử viên gạch dạng hình thoi là hình thoi ABCD có.
AB = 40 cm; O là giao điểm của AC và BD
Xét \(\Delta DAB\) có: AB = AD = 40 cm; \( \Rightarrow \Delta DAB\) là tam giác đều suy ra
BD = AB = AD = 40cm \( \Rightarrow OB = \dfrac{{BD}}{2} = \dfrac{{40}}{2} = 20cm\)
Xét \(\Delta AOB\) vuông tại O có: \(O{A^2} + O{B^2} = A{B^2} \Rightarrow O{A^2} = A{B^2} - O{B^2} = {40^2} - {20^2} = 1200\)
\( \Rightarrow OA = \sqrt {1200} \Rightarrow AC = 2\sqrt {1200} \)
Diện tích của hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.40.2\sqrt {1200} = 1385,64(c{m^2})\)
Vậy diện tích của viên gạch đó là: \(1385,64(c{m^2})\)