Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)Ảnh thật.
c)Để ảnh thật cao gấp đôi vật \(\Rightarrow h'=2h\) thì:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{2h}=\dfrac{d}{d'}=\dfrac{1}{2}\Rightarrow d'=2d\)
Khi đó vị trí cách thấu kính là:
\(d'=2d=2\cdot50=100cm\)

Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải: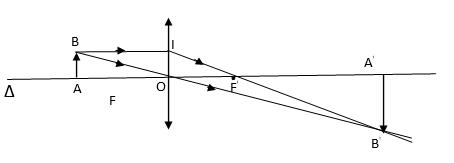
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm

a)Bạn tự vẽ hình nha!!!
Ảnh thật, ngược chiều, và lơn hơn vật.
b)Khỏang cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{15}{30}\Rightarrow h'=4cm\)

AB = 2cm
OA = 15cm
OF = 10cm
a. Hình vẽ tham khảo ảnh
b. Ta có 1/A'O = 1/OF - 1/AO = 1/10 - 1/15 = 1/30 hay A'O = 30cm
Vì A'B'/AB = A'O/AO nên A'B' = (AB.A'O)/AO = (2.30)/15 = 4cm
Vậy ảnh cao 4cm và cách thấu kính một đoạn 30cm
(Cách chứng minh như trong hình vẽ)

a) Ảnh thật vì d > f
b)
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{2}{A'B'}=\dfrac{15-10}{10}\)
=> A'B' = 4cm
\(\Delta ABO\sim\Delta A'B'O\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow OA'=\dfrac{OA.A'B'}{AB}=\dfrac{15.4}{2}=30cm\)