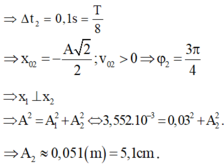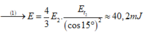Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một con lắc lò xo dao động theo phương trình x = 4cos10t
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}m.w^2.A^2=8.10^{-3}=8\left(mJ\right)\)
Vậy C đúng
Thế năng cực đại của con lắc lò xo:
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}.m.\omega^2.A^2=8.10^{-3}=8mJ\)
Chọn C

Vận tốc cực đại: \(v_{max}=\sqrt{\dfrac{2W_{đmax}}{m}}=\sqrt{\dfrac{2.0,1}{0,2}}=1m/s\)
Khi \(W_{đ1}=0,025J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,025}{0,2}}=0,5m/s\)
Khi \(W_{đ2}=0,75J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,075}{0,2}}=0,5\sqrt 3m/s\)
Vì vận tốc biến thiên điều hoà theo thời gian, nên ta biểu diễn bằng véc tơ quay:
v O 1 0,5 0,5√3 30 0
Từ giản đồ véc tơ ta suy ra được: \(\Delta t=\dfrac{30}{360}T=\dfrac{\pi}{20}\)
\(\Rightarrow T =\dfrac{3\pi}{5}s\)
\(\Rightarrow \omega = \dfrac{2\pi}{T}=\dfrac{10}{3}\) (rad/s)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=0,3m = 30cm\)

Khi \(W_đ=\dfrac{W_{đmax}}{4}\)
\(\Rightarrow v = \dfrac{v_{max}}{2}\)
Thời gian vận tốc biến thiên từ 0 đến \( \dfrac{v_{max}}{2}\) là \(\dfrac{T}{12}\) (véc tơ quay đã quay 1 góc 300)
\(\Rightarrow \dfrac{T}{12}=\dfrac{1}{6}\Rightarrow T = 2s\)
\(\Rightarrow f = 2\pi/T = 1(Hz)\)
Vậy trong 1s vật thực hiện 1 dao động.

Đáp án A
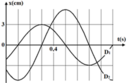
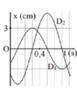
Ta có 1 ô ⇔ 0 , 4 s ⇒ 1 ô = 0,1 s
![]()
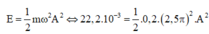
=> A = 0,06 m = 6 cm
Thấy 2 đỉnh của D 1 v à D 2 cách nhau 2 ô (1T là 8 ô)=> D 1 v à D 2 vuông pha:
A 2 = A 1 2 + A 2 2 ⇒ A 2 = 6 2 - 3 2 = 3 3 = 5 , 19 c m

- Ta có: 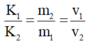
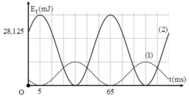
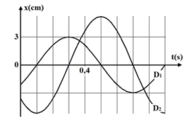
- Từ đồ thị ta thấy: A1 = 3 cm.
- Cũng theo đồ thị thì ta thấy cứ một ô ngang theo trục thời gian là 0,1s.
- Quan sát đồ thị ta thấy thời gian dao động D2 đi từ VTCB ra biên mất thời gian là 2 ô nên:
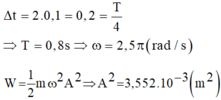
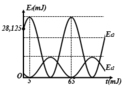
- Gọi Δ1 là thời gian kể từ lúc D1 bắt đầu dao động đến khi lần đầu tiên qua VTCB:
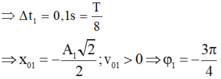
- Gọi Δ2 là thời gian kể từ lúc D2 bắt đầu dao động đến khi lần đầu tiên đến biên âm: