Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo công thức của chuyển động quay biến đổi đều
\(\omega^2-\omega^2_0=2.\gamma.\varphi\)
\(\left(\omega-\omega_0\right).\left(\omega+\omega_0\right)=2.\frac{\left(\omega-\omega_0\right)}{t}.\varphi\)
\(\left(\omega+\omega_0\right).t=2.\varphi\)
Với \(t=30s\), \(\omega=20\pi\) và \(\varphi=360\pi\)
suy ra
\(\omega_0=4.\pi\) rad/s và \(\gamma=16\pi\text{ /}30\) rad/s2
Thời gian để đạt được tốc độ \(\omega_0\) từ trạng thái nghỉ là \(\omega_0\text{π /}\gamma\) = 7.5 s
Phương trình chuyển động của bánh xe từ trạng thái nghỉ là
\(\varphi\)= (1/2 ). (16\(\pi\)/30).t2 rad

Giải thích: Đáp án A
Phương pháp:
- Áp dụng công thức tính vận tốc và quãng đường của vật trong chuyển động thẳng nhanh dần đều
- Áp dụng định luật II Niuton
Cách giải:
- Tần số góc: 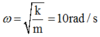
- Vật chuyển động nhanh dần đều cùng ván, khi bắt đầu rời khỏi tấm ván, vận tốc và quãng đường vật đi
được lúc đó là: 
- Khi vật rời ván, áp lực do vật tác dụng lên ván bằng 0 nên chỉ còn lực đàn hồi và trọng lực tác dụng lên tấm ván.
ADĐL II Niuton ta được: 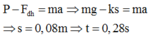

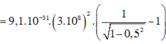
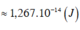



Câu C nha
C