Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì số bi trong hộp thứ nhất và hộp thứ hai là độc lập và việc lấy ra số các bi từ hai hộp là độc lập nên hai biến cố A, B là độc lập.
b)
- Trên A:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_3}{C^2_5}=\frac{3}{10}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_3+C^2_2}{C^2_5}=\frac{4}{10}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{4}{10}=\frac{6}{10}\).
- Trên B:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_4}{C^2_{10}}=\frac{2}{15}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_4+C^2_6}{C^2_{10}}=\frac{7}{15}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{7}{15}=\frac{8}{15}\).

a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)

Đáp án C.
Số cách lấy ngẫu nhiên 4 quả là: C 10 4 (cách)
Số cách lấy được 2 quả đỏ, 2 trắng là: C 4 2 . C 7 2 (cách)
Xác suất để lấy được đúng 2 quả đỏ là:
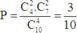

Chọn A
Gọi T là phép thử lấy mỗi hộp ra một quả. Số phần tử của không gian mẫu trong phép thử T là![]()
Gọi A là biến cố hai quả lấy ra từ mỗi hộp đều là màu đỏ. Số phần tử của biến cố A là: ![]() .
.
Vậy xác suất của biến cốA là 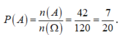 .
.

Chọn A
Ta có ![]()
Gọi A là biến cố “lấy được 3 quả cầu màu xanh”.![]()
Nên 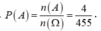


Không gian mẫu \(n\left(\Omega\right)=C_{20}^3=1140\)
a/ Gọi A là biến cố "lấy được một quả đỏ, một quả trắng, một quả xanh":
\(n\left(A\right)=C_5^1.C^1_7.C^1_8=5.7.8=280\) \(\Rightarrow\)\(P\left(A\right)=\dfrac{280}{1140}=\dfrac{14}{57}\)
b/ Chắc bạn chép sai đề, chỉ lấy 3 quả mà lại còn ít nhất cả ba đều đỏ thì người ta ghi luôn là "cả 3 quả đều đỏ" có gọn hơn không? Mình đoán đề gốc là "lấy được ít nhất một quả màu đỏ". Quyết định làm cả 2 trường hợp:
- Nếu đề yêu cầu cả 3 quả đều đỏ \(\Rightarrow n\left(B\right)=C_5^3=10\) \(\Rightarrow\)xác suất \(P\left(B\right)=\dfrac{10}{1140}=\dfrac{1}{114}\)
- Nếu đề yêu cầu ít nhất một quả đỏ:
Gọi C là biến cố "lấy được ít nhất một quả đỏ" \(\Rightarrow\overline{C}\) là biến cố "không lấy được quả đỏ nào"
\(n\left(\overline{C}\right)=C_{15}^3=455\)
\(\Rightarrow n\left(C\right)=n\left(\Omega\right)-n\left(\overline{C}\right)=1140-455=685\) \(\Rightarrow\)\(P\left(C\right)=\dfrac{685}{1140}=\dfrac{137}{228}\)