Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
+ E = 1 2 kA2 = 0,5J (nhớ đổi đơn vị của A).
+ Chất điểm ở M nhận cùng một li độ và ngược chiều nhau,ta có hình minh họa. Từ hình vẽ => x = ± A/2.
+ Wđ = 3Wt
(dùng công thức Wđ = nWt ⇔ x = ± A n + 1 )
=> Wđ = 3 4 E = 0,375J = 375mJ.
△t=\(\dfrac{5T}{6}=\dfrac{T}{6}+\dfrac{T}{2}+\dfrac{T}{6}\) => S= \(\dfrac{A}{2}+2A+\dfrac{A}{2}\)
=> vị trí M có li độ x=\(\dfrac{A}{2}=5\left(cm\right)\)
=> Wđ =W-Wt=\(\dfrac{1}{2}k.A^2-\dfrac{1}{2}kx^2=0,375\left(J\right)\)
Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)
Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)
Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5
Thời gian quả cầu đi từ vị trí cao nhất (x = -A) đến vị trí thấp nhất (x = A) chính là \(\frac{T}{2} = 0,2 => T = 0,4s.\)
Lực đàn hồi của lò xo khi lò xo ở vị trí thấp nhất chính là \(F_{dhmax} = k(A+\Delta l)\)
\(\frac{F_{max}}{P} = \frac{k(A+\Delta l)}{mg} = \frac{kA+k\Delta l }{mg } = 1+\frac{kA}{mg} =\frac{7}{4}\) (do \(k\Delta l = mg\))
=> \(A = \frac{3g}{4}\frac{m}{k} = \frac{3g}{4}.\frac{T^2}{4\pi^2} =0,03m = 3cm.\)
Đáp án D
Từ thời điểm t đến thời điểm t +
T
4
thì góc quay thêm là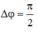 
ở thời điểm t + T 4
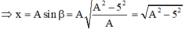luôn có
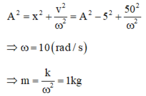
Đáp án A
Phương pháp: Sử dụng vòng tròn lượng giác và định luật bảo toàn cơ năng
Cách giải:
Sử dụng đường tròn biểu diễn vị trí tương ứng M1 và M2 với vật dao động điều hòa khi có li độ M nhưng theo 2 chiều ngược nhau.
(Cung lớn từ M1 sang M2).
OM1 hợp với trục Ox 1 góc π 3 như hình vẽ
=> Điểm M có li độ x = A/2 = 5 cm
=> Động năng của vật khi đi qua vị trí M là: