




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Ta có các quy luật sau:
\(\left(1+3\right)-2=2\)
\(\left(2+2\right)-3=1\)
\(\left(5+5\right)-6=4\)
Vậy dòng cuối là:
\(\left(5+9\right)-5=9\)
Số điền vào là 9
(Quy luật: lấy 2 số phía dưới cộng với nhau rồi trừ cho số phía trên sẽ ra được số ở giữa)

Quy luật: Hiệu của số lớn hơn trừ cho số nhỏ hơn trong mổi ô chính là kết quả của ô màu vàng đối diện
17-13=4
15-6=9
14-8=6
19-12=7
23-15=8
27-25=2
23-18=5
Suy ra: 12-x=3
=> x=12-3=9
Đáp án C
Giải thích: Mỗi số trong hình tam giác màu vàng bằng số lớn hơn của hình bình hành đối diện trừ đi số bé hơn ở hình bình hành đối diện.
=> ? - 12 = 3 hoặc 12 - ? = 3
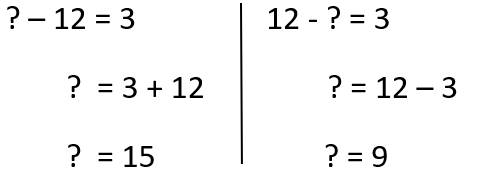
=> Đáp án là 15 hoặc 9
Đáp án: c
Bổ sung: Đáp án cũng có thể là 15

20.
4^n=256
4^n=4^4
n=4
9^5n-8=81
9^5n-8=9^2
5n-8=2
5n=10
n=2
3^n+2:27=3
3^n+2:3^3=3
3^n+2-3=3
n+2-3=1
n=2
8^n+2.2^3=8^5
8^n+2.8=8^5
8^n+2+1=8^5
n+2+1=5
n=2
21.
30-2x^2=12
2x^2=30-12
2x^2=18
x^2=9
x^2=3^2
x=3
(9-2x)^3=125
(9-2x)^3=5^3
(9-2x)=5
2x=4
x=2
(2x-2)^4=0
(2x-2)=0
2x=2
x=1
(x+5)^3=(2x)^3
x+5=2x
x+5-2x=0
(x-2x)=-5
-x=-5
x=5
20:
a: \(4^{n}=256\)
=>\(4^{n}=4^4\)
=>n=4
b: \(9^{5n-8}=81\)
=>\(9^{5n-8}=9^2\)
=>5n-8=2
=>5n=10
=>n=2
c: \(3^{n+2}:27=3\)
=>\(3^{n+2}=27\cdot3=81=3^4\)
=>n+2=4
=>n=2
d: \(8^{n+2}\cdot2^3=8^5\)
=>\(8^{n+2}=8^5:8=8^4\)
=>n+2=4
=>n=2
Bài 21:
a: \(30-2x^2=12\)
=>\(2x^2=30-12=18\)
=>\(x^2=9\)
mà x>=0(do x là số tự nhiên)
nên x=3
b: \(\left(9-2x\right)^3=125\)
=>9-2x=5
=>2x=4
=>x=2
c: \(\left(2x-2\right)^4=0\)
=>2x-2=0
=>2x=2
=>x=1
d: \(\left(x+5\right)^3=\left(2x\right)^3\)
=>2x=x+5
=>2x-x=5
=>x=5

20.
a.
\(4^{n}=256\)
\(4^{n}=4^4\)
\(n=4\)
b.
\(9^{5n-8}=81\)
\(9^{5n-8}=9^2\)
5n-8=2
5n=10
n=2
c.
\(3^{n+2}:27=3\)
\(3^{n+2}=27.3\)
\(3^{n+2}=81\)
\(3^{n+2}=3^4\)
n+2=4
n=2
d.
\(8^{n+2}.2^3=8^5\)
\(8^{n+2}=8^5:2^3\)
\(8^{n+2}=8^4\)
n+2=4
n=2
21.
a.
\(30-2x^2=12\)
\(2x^2=30-12\)
\(2x^2=18\)
\(x^2=18:2=9\)
\(x^2=3^2\)
\(x=\pm3\)
b.
\(\left(9-2x\right)^3=125\)
\(\left(9-2x\right)^3=5^3\)
\(9-2x=5\)
2x=9-5=4
x=2
c.
\(\left(2x-2\right)^4=0\)
2x-2=0
2x=2
x=1
d.
\(\left(x+5\right)^3=\left(2x\right)^3\)
x+5=2x
2x-x=5
x=5

a) \(M=1+2+2^2+2^3+\cdots+2^{100}\)
\(2M=2+2^2+2^3+2^4+\cdots+2^{101}\)
\(2M-M=\left(2+2^2+2^3+2^4+\cdots+2^{101}\right)-\left(1+2+2^2+2^3+\cdots+2^{100}\right)\)
\(\Rightarrow M=2^{101}-1\)
Vậy \(M=2^{101}-1\)
b) \(N=1+3^2+3^4+3^6+\cdots+3^{100}\)
\(3N=3+3^2+3^4+3^6+3^8+\cdots+3^{102}\)
\(3N-N=\left(3+3^2+3^4+3^6+3^8+\cdots+3^{102}\right)-\left(1+3+3^2+3^4+3^6+\cdots+3^{100}\right)\)
\(\Rightarrow2N=3^{102}-1\)
\(\Rightarrow N=\frac{3^{102}-1}{2}\)
Vậy \(N=\frac{3^{102}-1}{2}\)
c) \(P=1+5^3+5^6+5^9+\cdots+5^{99}\)
\(5^3\cdot P=5^3+5^6+5^9+5^{12}\cdots+5^{102}\)
\(125P-P=\left(5^3+5^6+5^9+5^{12}\cdots+5^{102}\right)-\left(1+5^3+5^6+5^9+\cdots+5^{99}\right)\)
\(\Rightarrow124P=5^{102}-1\)
\(\Rightarrow P=\frac{5^{102}-1}{124}\)
Vậy \(P=\frac{5^{102}-1}{124}\)
a: \(M=1+2+2^2+\cdots+2^{100}\)
=>\(2M=2+2^2+2^3+\cdots+2^{101}\)
=>\(2M-M=2+2^2+2^3+\cdots+2^{101}-1-2-\cdots-2^{100}\)
=>\(M=2^{101}-1\)
b: \(N=1+3^2+3^4+\cdots+3^{100}\)
=>\(9N=3^2+3^4+3^6+\cdots+3^{102}\)
=>\(9N-N=3^2+3^4+\cdots+3^{102}-1-3^2-\cdots-3^{100}\)
=>\(8N=3^{102}-1\)
=>\(N=\frac{3^{102}-1}{8}\)
c: \(P=1+5^3+5^6+\cdots+5^{99}\)
=>\(125P=5^3+5^6+5^9+\cdots+5^{102}\)
=>\(125P-P=5^3+5^6+\cdots+5^{102}-1-5^3-\cdots-5^{99}\)
=>\(124P=5^{102}-1\)
=>\(P=\frac{5^{102}-1}{124}\)

a: \(M=1+2+2^2+\cdots+2^{100}\)
=>\(2M=2+2^2+2^3+\cdots+2^{101}\)
=>\(2M-M=2+2^2+2^3+\cdots+2^{101}-1-2-\cdots-2^{100}\)
=>\(M=2^{101}-1\)
b: \(N=1+3^2+3^4+\cdots+3^{100}\)
=>\(9N=3^2+3^4+3^6+\cdots+3^{102}\)
=>\(9N-N=3^2+3^4+\cdots+3^{102}-1-3^2-\cdots-3^{100}\)
=>\(8N=3^{102}-1\)
=>\(N=\frac{3^{102}-1}{8}\)
c: \(P=1+5^3+5^6+\cdots+5^{99}\)
=>\(125P=5^3+5^6+5^9+\cdots+5^{102}\)
=>\(125P-P=5^3+5^6+\cdots+5^{102}-1-5^3-\cdots-5^{99}\)
=>\(124P=5^{102}-1\)
=>\(P=\frac{5^{102}-1}{124}\)

\(3^{x-5}=27\)
<=> \(3^{x-5}=3^3\)
=> x - 5 = 3
=> x = 8
Vậy x = 8

Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)