Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)

a: Xét ΔKAD và ΔBDA có
\(\hat{KAD}=\hat{BDA}\) (hai góc so le trong, AK//BD)
AD chung
\(\hat{KDA}=\hat{BAD}\) (hai góc so le trong, AB//CD)
Do đó: ΔKAD=ΔBDA
=>KA=BD
mà BD=AC
nên AK=AC
=>ΔAKC cân tại A
b: ΔAKC cân tại A
=>\(\hat{AKC}=\hat{ACK}\)
mà \(\hat{AKC}=\hat{BDC}\) (hai góc đồng vị, BD//AK)
nên \(\hat{BDC}=\hat{ACD}\)
Xét ΔBDC va ΔACD có
BD=AC
\(\hat{BDC}=\hat{ACD}\)
CD chung
Do đó: ΔBDC=ΔACD
=>\(\hat{BCD}=\hat{ADC}\)
=>ABCD là hình thang cân

\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)

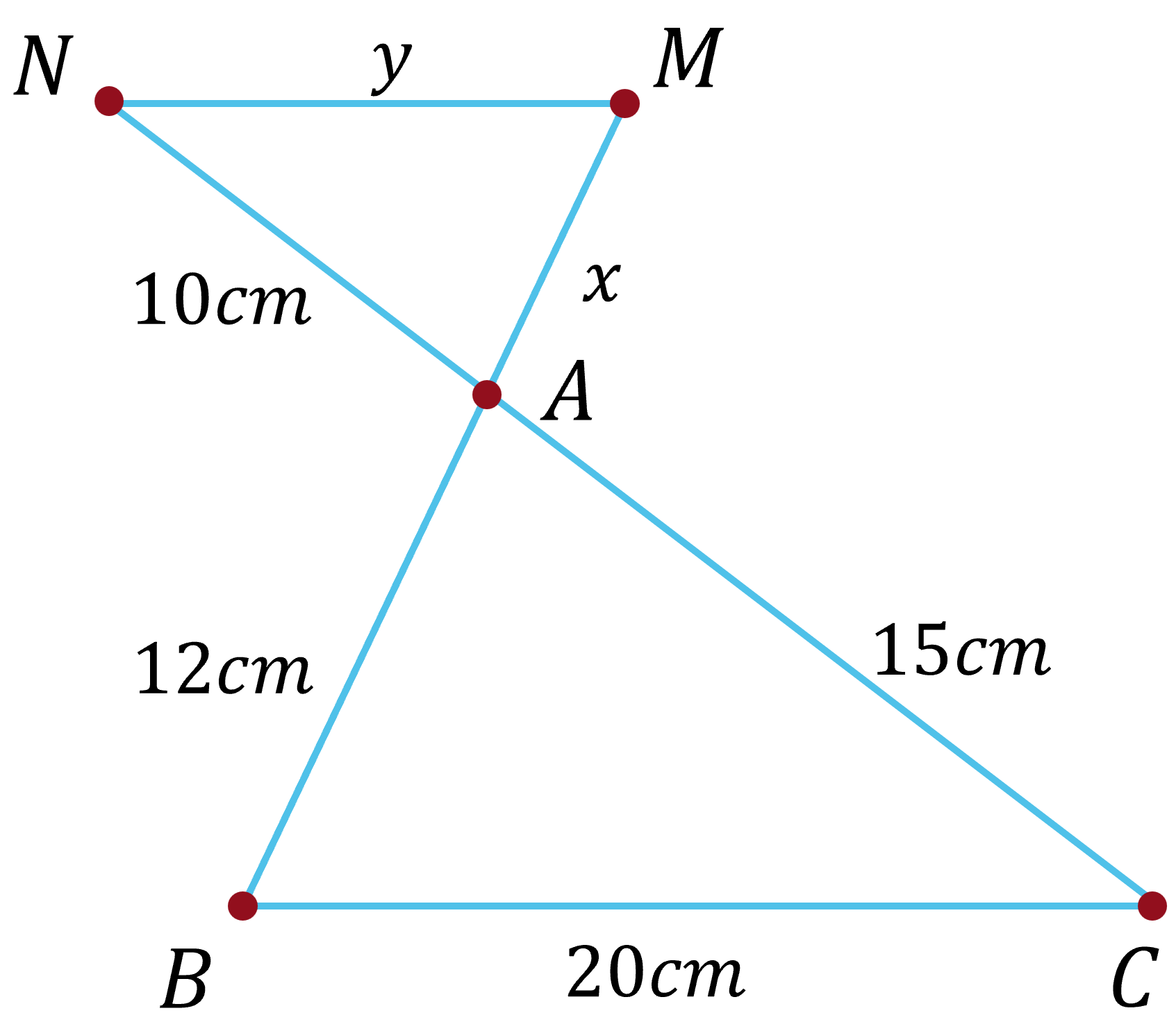
Vì MN // BC theo Talet ta có:
\(\dfrac{y}{20}\) = \(\dfrac{10}{15}\) = \(\dfrac{x}{12}\) => x = \(\dfrac{10}{15}\) . 12 = 8; y = \(\dfrac{10}{15}\) . 20 = \(\dfrac{40}{3}\)

1B:
a: \(x^2+2xy+x+2y\)
=x(x+2y)+(x+2y)
=(x+2y)(x+1)
b: \(2xy+yz+2x+z\)
=y(2x+z)+(2x+z)
=(2x+z)(y+1)
c: \(y^2-2y-z^2-2z\)
\(=\left(y^2-z^2\right)-2\left(y+z\right)\)
=(y+z)(y-z)-2(y+z)
=(y+z)(y-z-2)
d: \(x^3-x-y+y^3\)
\(=\left(x^3+y^3\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2-1\right)\)
2A:
a: \(x^2-2x+1-y^2\)
\(=\left(x-1\right)^2-y^2\)
=(x-1-y)(x-1+y)
b: \(x^2-y^2+4y-4\)
\(=x^2-\left(y^2-4y+4\right)\)
\(=x^2-\left(y-2\right)^2\)
=(x-y+2)(x+y-2)
c: \(y^2+6y-4z^2+9\)
\(=\left(y^2+6y+9\right)-\left(2z\right)^2\)
\(=\left(y+3\right)^2-\left(2z\right)^2=\left(y+3+2z\right)\left(y+3-2z\right)\)
d: \(x^2-y^2+10yz-25z^2\)
\(=x^2-\left(y^2-10yz+25z^2\right)\)
\(=x^2-\left(y-5z\right)^2=\left(x-y+5z\right)\left(x+y-5z\right)\)
2B:
a: \(4x^2-4x+1-25y^2\)
\(=\left(4x^2-4x+1\right)-\left(5y\right)^2\)
\(=\left(2x-1\right)^2-\left(5y\right)^2=\left(2x-1-5y\right)\left(2x-1+5y\right)\)
b: \(9y^2-z^2+6z-9\)
\(=\left(3y\right)^2-\left(z^2-6z+9\right)\)
\(=\left(3y\right)^2-\left(z-3\right)^2\)
=(3y-z+3)(3y+z-3)
c: \(x^2-4z^2+4x+4\)
\(=\left(x^2+4x+4\right)-\left(2z\right)^2\)
\(=\left(x+2\right)^2-\left(2z\right)^2\)
=(x+2+2z)(x+2-2z)
d: \(4x^2-y^2+4xz+z^2\)
\(=\left(4x^2+4xz+z^2\right)-y^2\)
\(=\left(2x+z\right)^2-y^2\)
=(2x+z-y)(2x+z+y)
3A:
a: \(x^2-2xy+y^2-a^2+2ab-b^2\)
\(=\left(x^2-2xy+y^2\right)-\left(a^2-2ab+b^2\right)\)
\(=\left(x-y\right)^2-\left(a-b\right)^2\)
=(x-y-a+b)(x-y+a-b)
c: \(x^3+y^3+3x^2-3xy+3y^2\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3\left(x^2-xy+y^2\right)\)
\(=\left(x^2-xy+y^2\right)\left(x+y+3\right)\)





.png)




a: =x^2+6x+9+x^2-6x+9+2x^2-32
=4x^2-14
b: =(x+3-10+x)^2=(2x-7)^2=4x^2-28x+49
c: =(x-3-x+5)^2=2^2=4
e: =x^2+10x+25-x^2+10x-25=20x
d: A=(5-1)(5+1)(5^2+1)(5^4+1)/4
=(5^2-1)(5^2+1)(5^4+1)/4
=(5^4-1)(5^4+1)/4
=(5^8-1)/4
g: =x^2-9-x^2-4x+5
=-4x-4