Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi A là biến cố xảy ra trường hợp để yêu cầu.Không gian mẫu
Xét các trường hợp có thể xảy ra biến cố A là.
+) 2 nam Toán, 2 nữ Lý: C 8 2 . C 7 2 = 588
+) 2 nữ Toán, 2 nam Lý: C 7 2 . C 5 2 = 210
+) 1 nam Toán, 1 nam Lý, 1 nữ Toán, 1 nữ Lý
C 7 1 . C 5 1 . C 7 1 . C 8 1 = 1960
Số cách chọn cần tìm
Xác suất cần tìm là. 197 495
Ta thực hiện các công đoạn sau:
Bước 1: Chọn 1 nam trong 7 nam làm tổ trưởng, có 
cách.
Bước 2: Chọn 1 nữ trong 6 nữ làm thủ quỹ, có 
cách.
Bước 3: Chọn 1 tổ phó trong 11 bạn còn lại (bỏ 2 bạn đã chọn ở bước 1 và bước 2), có 
cách.
Bước 4: Chọn 2 tổ viên trong 10 bạn còn lại (loại 3 bạn đã chọn ở trên), có 
cách.
Theo quy tắc nhân có 
cách chọn một tổ thỏa yêu cầu.
Chọn A
Chọn C.
Số phần tử của của không gian mẫu: 
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
Chọn C.
Số phần tử của của không gian mẫu: 
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có 
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có 
cách.
Do đó trường hợp này có 
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có 
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có 
cách.
Do đó trường hợp này có 
cách.
Suy ra số phần tử của biến cố là 
Vậy xác suất cần tính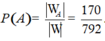 
Chọn C.
Chọn 2 trong 15 nam làm tổ trưởng và tổ phó có A 15 2 cách.
sau khi chọn 2 nam thì còn lại 13 bạn nam. Chọn 3 tổ viên, trong đó có nữ.
+) chọn 1 nữ và 2 nam có 5 . C 13 2 cách.
+) chọn 2 nữ và 1 nam có 13 . C 5 2 cách.
+) chọn 3 nữ có C 5 3 cách.
Vậy có A 15 2 ( 5 . C 13 2 + 13 . C 5 2 + C 5 3 ) = 111300 cách.
Chọn D.
Số cách chọn 4 học sinh làm 4 tổ trưởng là: 
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là 
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là: 
Vậy số cách chọn thỏa yêu cầu bài toán: 
Chọn C.
Nếu mà không quá 1 em nữ => Không có em nữ nào tham gia.
=> 5 em trên là 5 em nam và chỉ có 1 cách chọn.
Số thành viên nữ của tố `23` là: `60. 5/12=25` (thành viên)
`=>` Số thành viên nam của tổ `23` là: `60-25=35` (thành viên)
`@TH1:` Chọn `3` giáo viên mà không có tổ trưởng
`=>` Có `C_25 ^2 .C_33^1 +C_25 ^1 .C_33^2=23100` cách
`@TH2:` Chọn `3` thành viên trong đó có `1` tổ trưởng là `1` trong `2` tổ trưởng nam.
`=>` Có `2.C_25 ^2=600` cách
`@TH3:` Chọn `3` thành viên trong đó có cả `2` tổ trưởng
`=>` Có `1.C_25 ^1=25` cách
`=>` Có tất cả `23100+600+25=23725` cách
`->bb B`