BT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
5
27 tháng 8
Bài 23:
a+4b⋮13
=>10(a+4b)⋮13
=>10a+40b⋮13
=>10a+b+39b⋮13
mà 39b⋮13
nên 10a+b⋮13
NQ
Nguyễn Quốc Đạt
CTVVIP
14 tháng 10 2023
a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 10 2023
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
29 tháng 1 2024
Chiều rộng của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) : \(\dfrac{7}{3}\) = \(\dfrac{9}{4}\) (m)
Chu vi của mảnh vườn hìn chữ nhật là:
(\(\dfrac{21}{4}\) + \(\dfrac{9}{4}\)) x 2 = 15 (m)
Diện tích của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) x \(\dfrac{9}{4}\) = \(\dfrac{189}{16}\) (m2)
b; Số tiền thu được khi trồng hoa để bán trên mảnh đất hình chữ nhật đó là:
80 000 x \(\dfrac{189}{16}\) = 945 000 (đồng)
KL...
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
29 tháng 1 2024
Bài 5:
a, Chiều rộng mảnh vườn:
\(\dfrac{21}{4}:\dfrac{7}{3}=\dfrac{9}{4}\left(m\right)\)
Chu vi mảnh đất:
\(2\times\left(\dfrac{21}{4}+\dfrac{9}{4}\right)=15\left(m\right)\)
Diện tích mảnh đất:
\(\dfrac{21}{4}\times\dfrac{9}{4}=\dfrac{189}{16}\left(m^2\right)\)
b, Số tiền thu được khi bán hoa:
\(\dfrac{189}{16}\times80000=945000\left(đồng\right)\)
23 tháng 8
bài 3:
a: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=5\left(1+5+5^2+\cdots+5^{19}\right)\) ⋮5
b: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{19}+5^{20}\right)\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdots+5^{19}\left(1+5\right)\)
\(=6\left(5+5^3+\cdots+5^{19}\right)\) ⋮6
c: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+\cdots+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\)
\(=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)+\cdots+5^{17}\left(1+5+5^2+5^3\right)\)
\(=\left(1+5+5^2+5^3\right)\left(5+5^5+\cdots+5^{17}\right)=156\cdot\left(5+5^5+\cdots+5^{17}\right)\)
\(=13\cdot12\cdot\left(5+5^5+\cdots+5^{17}\right)\) ⋮13
Bài 2:
a: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=3\left(1+3+3^2+3^3+\cdots+3^{119}\right)\) ⋮3
b: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+\cdots+\left(3^{119}+3^{120}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+\cdots+3^{119}\left(1+3\right)\)
\(=4\left(3+3^3+\cdots+3^{119}\right)\) ⋮4
c: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\cdots+\left(3^{118}+3^{119}+3^{120}\right)\)
\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+\cdots+3^{118}\left(1+3+3^2\right)\)
\(=13\left(3+3^4+\cdots+3^{118}\right)\) ⋮13
Bài 1:
a: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=2\left(1+2+2^2+\cdots+2^{19}\right)\) ⋮2
b: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\cdots+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+\cdots+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+\cdots+2^{19}\right)\) ⋮3
c: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\cdots+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+\cdots+2^{17}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+\ldots+2^{17}\right)=5\cdot3\cdot\left(2+2^5+\cdots+2^{17}\right)\) ⋮5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 8
Bài 1:
a; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
A = 2 x (1+ 2+ 2\(^2\) + ... + 2\(^{19}\))
A ⋮ 2(đpcm)
b; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2;...; 20 đây là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(20 - 1) : 1+ 1 = 20(số)
Vì 20 : 2 = 10
Vậy nhóm hai số hạng liên tiếp của A vào nhau khi đó ta có:
A = (2+ 2\(^2\)) + (2\(^3\) + 2\(^4\)) + ... + (2\(^{19}+\) 2\(^{20}\))
A = 2.(1 + 2) + 2\(^3\).(1+ 2) + ... + 2\(^{19}\) .(1 + 2)
A = 2.3 + 2\(^3\).3 + ... + 2\(^{19}\).3
A = 3.(2+ 2\(^3\) + ... + 2\(^{19}\))
A ⋮ 3 (đpcm)
c; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2; 3;...; 20
Dãy số trên có 20 số hạng:
Vì 20 : 4 = 5
Vậy nhóm 4 hạng tử của A thành một nhóm khi đó:
A = (2+ 2\(^2\) + 2\(^3\) + 2\(^4\)) + ... + (2\(^{17}+2^{18}+2^{19}+2^{20}\))
A = 2.(1 + 2 + 2\(^2\) + 2\(^3\)) + ... + 2\(^{17}\).(1 + 2 + 2\(^2\) + 2\(^3\))
A = (1+ 2 +2\(^2\) + 2\(^3\)).(2+ ...+ 2\(^{17}\))
A = (1 + 2 + 4 + 8).(2+ ...+ 2\(^{17}\))
A = (3+ 4 + 8).(2+ ...+ 2\(^{17}\))
A = (7 + 8)(2+ ...+ 2\(^{17}\))
A = 15.(2+ ...+ 2\(^{17}\))
A ⋮ 5(đpcm)
CC
2
27 tháng 8
Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
Câu 4:
a: \(x^3=125\)
=>\(x^3=5^3\)
=>x=5
b: \(11^{x+1}=121\)
=>\(11^{x+1}=11^2\)
=>x+1=2
=>x=2-1=1
c: \(\left(x-5\right)^3=27\)
=>\(\left(x-5\right)^3=3^3\)
=>x-5=3
=>x=3+5=8
d: \(4^5:4^{x}=16\)
=>\(4^{x}=4^5:16=4^5:4^2=4^3\)
=>x=3
e: \(5^{x-1}\cdot8=1000\)
=>\(5^{x-1}=1000:8=125=5^3\)
=>x-1=3
=>x=3+1=4
f: \(2^{x}+2^{x+3}=72\)
=>\(2^{x}+2^{x}\cdot8=72\)
=>\(2^{x}\cdot9=72\)
=>\(2^{x}=\frac{72}{9}=8=2^3\)
=>x=3
g: \(\left(3x+1\right)^3=343\)
=>\(\left(3x+1\right)^3=7^3\)
=>3x+1=7
=>3x=6
=>x=2
h: \(3^{x}+3^{x+2}=270\)
=>\(3^{x}+3^{x}\cdot9=270\)
=>\(10\cdot3^{x}=270\)
=>\(3^{x}=\frac{270}{10}=27=3^3\)
=>x=3
i: \(25^{2x+4}=125^{x+3}\)
=>\(\left(5^2\right)^{2x+4}=\left(5^3\right)^{x+3}\)
=>\(5^{4x+8}=5^{3x+9}\)
=>4x+8=3x+9
=>x=1
Câu 6:
1 giờ=3600 giây
Số tế bào hồng cầu được tạo ra sau mỗi giờ là:
\(25\cdot10^5\cdot3600=25\cdot36\cdot10^7=900\cdot10^7=9\cdot10^9\) =9 tỉ (tế bào)
S
subjects
CTVHS
28 tháng 8
câu 5:
a. \(16^{16}=\left(2^4\right)^{16}=2^{64}\)
\(64^{11}=\left(2^6\right)^{11}=2^{66}\)
vì \(2^{66}>2^{64}\) nên \(64^{11}>16^{16}\)
b. \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
\(5^{20}<5^{21}\Rightarrow625^5<125^7\)
c. \(3^{36}=\left(3^3\right)^{12}=27^{12}\)
\(5^{24}=\left(5^2\right)^{12}=25^{12}\)
\(27^{12}>25^{12}\Rightarrow3^{36}>5^{24}\)
NM
2
NQ
Nguyễn Quốc Đạt
CTVVIP
5 tháng 12 2023
2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
NQ
Nguyễn Quốc Đạt
CTVVIP
5 tháng 12 2023
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499
16 tháng 8
Ta có: \(10A=\frac{10^{21}-60}{10^{21}-6}=\frac{10^{21}-6-54}{10^{21}-6}=1-\frac{54}{10^{21}-6}\)
\(10B=\frac{10^{22}-60}{10^{22}-6}=\frac{10^{22}-6-54}{10^{22}-6}=1-\frac{54}{10^{22}-6}\)
Ta có: \(10^{21}-6<10^{22}-6\)
=>\(\frac{54}{10^{21}-6}>\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}<-\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}+1<-\frac{54}{10^{22}-6}+1\)
=>10A<10B
=>A<B
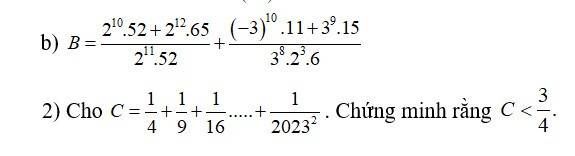
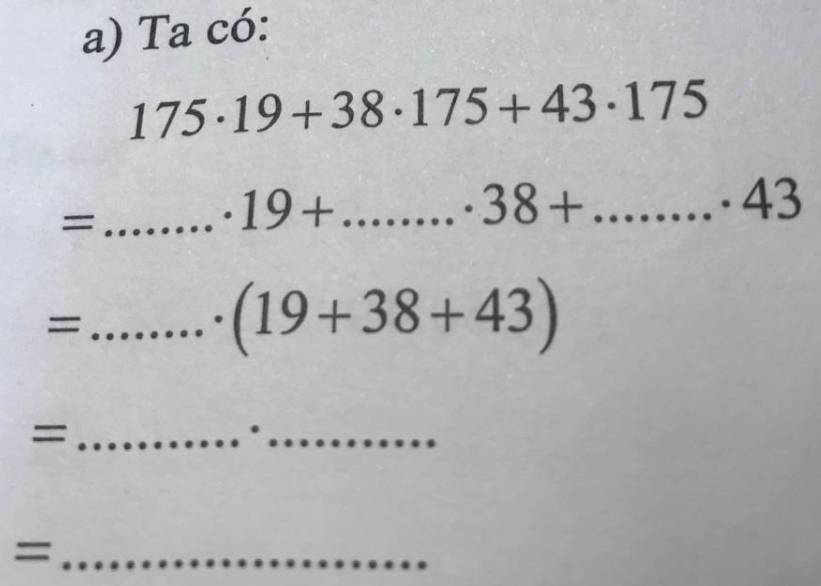
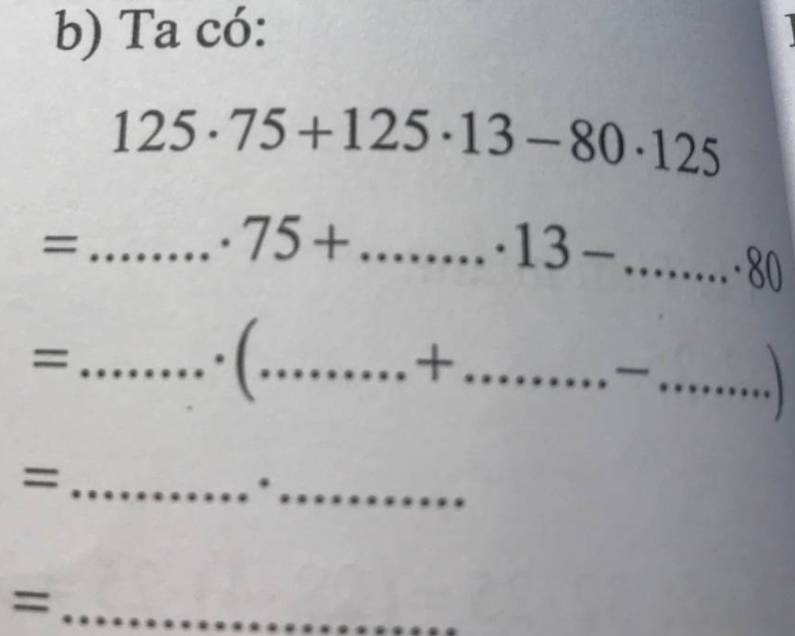
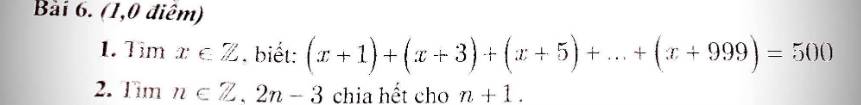
b) \(B=\dfrac{2^{10}\cdot52+2^{12}\cdot65}{2^{11}\cdot52}+\dfrac{\left(-3\right)^{10}\cdot11+3^9\cdot15}{3^8\cdot2^3\cdot6}\)
\(B=\dfrac{2^{10}\cdot2^2\cdot13+2^{12}\cdot5\cdot13}{2^{11}\cdot13\cdot2^2}+\dfrac{\left(-3\right)^{10}\cdot11+3^9\cdot3\cdot5}{3^8\cdot2^3\cdot2\cdot3}\)
\(B=\dfrac{2^{12}\cdot13+2^{12}\cdot13\cdot5}{2^{13}\cdot13}+\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}\)
\(B=\dfrac{2^{12}\cdot13\cdot\left(1+5\right)}{2^{13}\cdot13}+\dfrac{3^{10}\cdot\left(11+5\right)}{3^9\cdot2^4}\)
\(B=\dfrac{1+5}{2}+\dfrac{3\cdot16}{2^4}\)
\(B=3+3\)
\(B=6\)
cảm on bẹn nha