Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN ⊥ BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC ⊥ BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trực tâm của tam giác ABN
Suy ra: NE ⊥ AB
b. Ta có: MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: AF // NE
Mà NE ⊥ AB (chứng minh trên)
Suy ra: AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).
c. Trong tam giác ABN ta có: AN ⊥ BM và AM = MN
Suy ra tam giác ABN cân tại B
Suy ra BA = BN hay N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN (chứng minh trên)
Suy ra: FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn (B; BA).

cần hình ib mình mình gửi cho nhé =)
a)
Vì (O) và (O′) cắt nhau tại hai điểm A và B nên OO′ vuông AB ( định lý )
- Xét tam giác ADC
Có OO′ là đường trung bình ( vì O là trung điểm AC , O′ là trung điểm của AD)
Nên => OO′ // CD
=> AB vuông CD ( Quan hệ từ vuông góc đến song song )
Xét tam giác ADC
Có AC = AD ( vì hai đường tròn (O) và (O′) có cùng bán kính )
=> Tam giác ACD cân tại A có AB là đường cao nên AB cũng là đường trung tuyến
=> BC = BD hay cung BC = cung BD (vì (O) và (O′) là hai đường tròn bằng nhau )
b) Xét đường tròn (O′) có A , E , D cùng thuộc đường tròn và AD là đường kính nên tam giác AED vuông tại E
\(\Rightarrow DE\perp AC\Rightarrow\widehat{DEC}=90^o\)
- Xét \(\Delta DEC\)vuông tại E có B là trung điểm DC ( cmt )
\(\Rightarrow EB=\frac{DC}{2}=BD=EB\)
=> Cung EB = cung BD ( định lý )
Do đó B là điểm chính giữa cung ED

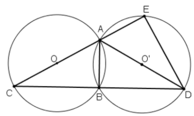
a) Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 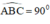
Chứng minh tương tự
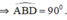
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 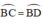 ( định lý )
( định lý )
b) Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ ![]()
⇒ ΔECD vuông tại E.
Ta có:
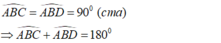
Suy ra: C, B, D thẳng hàng.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 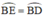 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
Kiến thức áp dụng
+ Với hai cung nhỏ trong cùng một đường tròn hoặc hai đường tròn bằng nhau thì hai dây bằng nhau căng hai cung bằng nhau.

a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
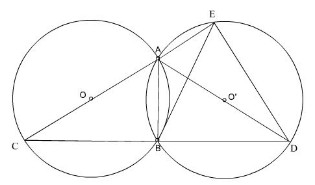
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD

b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD

cho hỏi điểm chính giữa cung là gì zậy!