Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình tham số của d là:
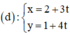
b) d nhận 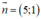 là 1 vec tơ pháp tuyến
là 1 vec tơ pháp tuyến
⇒ d nhận 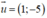 là 1 vec tơ chỉ phương
là 1 vec tơ chỉ phương
Phương trình tham số của đường thẳng d là:
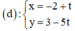

Lời giải:
a
VTPT: $(-2,5)$
PTĐT $(\Delta)$ là; $-2(x-1)+5(y-3)=0$
$\Leftrightarrow -2x+5y-13=0$
b. PTĐT $(\Delta)$ là:
$1(x-2)+4(y-1)=0\Leftrightarrow x+4y-6=0$
c.
VTCP của $(\Delta)$ là: $\overrightarrow{AB}=(2,5)$
$\Rightarrow$ VTPT của $(\Delta)$ là: $(-5,2)$
PTĐT $(\Delta)$ là: $-5(x-1)+2(y+2)=0$
$\Leftrightarrow -5x+2y+9=0$
d.
Làm tương tự câu c, PT $3x+2y-6=0$

a: Phương trìh tham số là:
\(\left\{{}\begin{matrix}x=3+4t\\y=5+t\end{matrix}\right.\)
vtcp là (4;1)
=>VTPT là (-1;4)
Phương trình tổng quát là:
-1(x-3)+4(y-5)=0
=>-x+3+4y-20=0
=>-x+4y-17=0
b: vtpt là (7;3)
=>VTCP là (-3;7)
Phương trình tham số là \(\left\{{}\begin{matrix}x=-2-3t\\y=4+7t\end{matrix}\right.\)
Phương trình tổng quát là:
7(x+2)+3(y-4)=0
=>7x+14+3y-12=0
=>7x+3y+2=0
c: vecto AB=(4;-4)
=>VTPT là (4;4)
Phương trình tham số là
x=1+4t và y=3-4t
Phương trình tổng quát là:
4(x-1)+4(y-3)=0
=>x-1+y-3=0
=>x+y-4=0

a) \(\left\{{}\begin{matrix}x=-5+4t\\y=-2-3t\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x=\sqrt{3}+2t\\y=1+3t\end{matrix}\right.\)

a) Phương trình tổng quát của đường thẳng d đi qua điểm \(A\left( { - 3;2} \right)\) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {2; - 3} \right)\) là: \(2\left( {x + 3} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 2x - 3y+12 = 0\)
Do vecto pháp tuyến là \(\overrightarrow n = (2; - \;3) \Rightarrow \overrightarrow u = (3;2)\)
Từ đó ta có phương trình tham số của đường thẳng d là:
\(\left\{ \begin{array}{l}x = - \;3 + 3t\\y = 2 + 2t\end{array} \right.\)\((t \in \mathbb{R})\)
b) Phương trình tham số của đường thẳng d đi qua điểm \(B\left( { - 2; - 5} \right)\) và có một vectơ chỉ phương là \(\overrightarrow u = \left( { - 7;6} \right)\) là: \(\left\{ \begin{array}{l}x = - 2 - 7t\\y = - 5 + 6t\end{array} \right.\left( {t \in \mathbb{R}} \right)\).
Từ đó ta có phương trình tổng quát của đường thẳng d là: \(\frac{{x + 2}}{{ - 7}} = \frac{{y + 5}}{6} \Leftrightarrow 6x + 7y + 47 = 0\).
c) Phương trình tổng quát của đường thẳng đi qua hai điểm \(C\left( {4;3} \right),D\left( {5;2} \right)\) là: \(\frac{{x - 4}}{{5 - 4}} = \frac{{y - 3}}{{2 - 3}} \Leftrightarrow x + y - 7 = 0\)
Từ đó ta có phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 7 - t\\y = t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\) .

a) Đường thẳng \(d\) đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 5 + t\end{array} \right.\)
Đường thẳng \(d\) có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {1; - 2} \right)\) và đi qua \(A( - 1;5)\)
Ta có phương trình tổng quát là
\((x + 1) - 2(y - 5) = 0 \Leftrightarrow x - 2y + 11 = 0\)
b) Đường thẳng \(d\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\), và đi qua điểm \(B(4; - 2)\) nên ta có phương trình tham số của \(d\) là :
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 2 + 3t\end{array} \right.\)
Đường thẳng \(d\) đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 4) - 2(y + 2) = 0 \Leftrightarrow 3x - 2y - 16 = 0\)
c) Đường thẳng \(d\) có dạng \(y = ax + b\)
d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\) nên ta có:
\(1 = - 2.1 + b \Rightarrow b = 3\)
Suy ra đồ thị đường thẳng d có dạng \(y = - 2x + 3\)
Vậy đường thẳng d có phương trình tổng quát là \(y + 2x - 3 = 0\)
Suy ra đường thẳng d có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\), nên có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 2} \right)\) và đi qua điểm \(P(1;1)\) nên ta có phương trình tham số của d là :
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 - 2t\end{array} \right.\)
d) Đường thẳng \(d\) đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {QR} = ( - 3;2)\) và có vectơ pháp tuyến \(\overrightarrow n = (2;3)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 3 - 3t\\y = 2t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(2(x - 3) + 3(x - 0) = \Leftrightarrow 2x + 3y - 6 = 0\)

Phương trình của ∆ là : y + 8 = -3(x + 5) <=> 3x + y + 23 = 0

Phương trình tham số d:
\(\left\{{}\begin{matrix}x=1+2t\\y=-4+3t\end{matrix}\right.\)
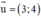 ;
;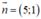

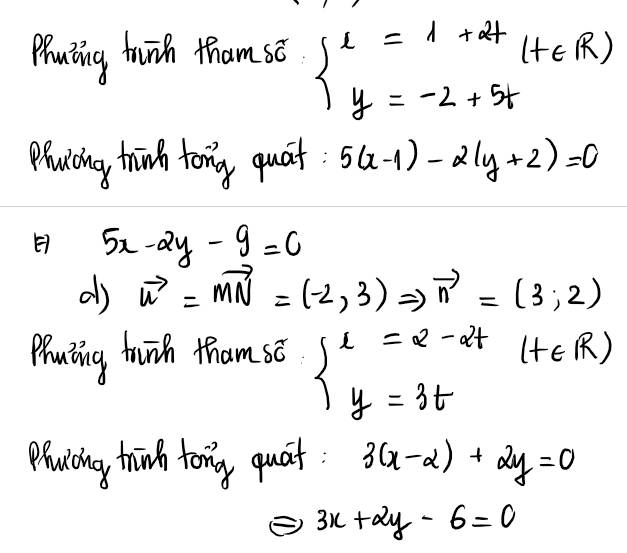
vì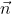 = (5; 1) nên ta chọn vectơ
= (5; 1) nên ta chọn vectơ 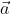 ⊥
⊥ 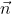 là vec tơ
là vec tơ 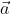 = (1; -5)
= (1; -5)
Từ đây ta có phương trình tham số của d: