
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc của ba bạn học sinh lần lượt là a, b, c (km/h) (Điều kiện: a, b, c > 0)
Ta có: b – a = 3. Đổi 30 phút = 1212 giờ.
Vì quãng đường ba bạn đi là như nhau nên theo đề bài ta có: a.12=b.25=c.49a.12=b.25=c.49
Vậy ta có: a2=2b5=4c9a2=2b5=4c9 và 2b – 2a = 6. Do đó 2a4=2b5=4c92a4=2b5=4c9 và 2b – 2a = 6
Theo tính chất dãy tỉ số bằng nhau ta có:
2a4=2b5=4c9=2b–2a5–4=61=62a4=6⇒a=4.62=12;2b5=6⇒b=5.62=15;4c9=6⇒c=9.64=13,52a4=2b5=4c9=2b–2a5–4=61=62a4=6⇒a=4.62=12;2b5=6⇒b=5.62=15;4c9=6⇒c=9.64=13,5
Vậy vận tốc của học sinh thứ nhất là 12 km/h
Quãng đường từ trường đến nhà thi đấu Quận là: 12.12=6(km).

Gọi độ dài quãng đường là x
Theo đề, ta có: Vận tốc của bạn 1,2,3 lần lượt là x/1/2; x/2/5 và x/4/9
Theo đề, ta có: \(x:\dfrac{2}{5}-x:\dfrac{1}{2}=3\)
=>2,5x-2x=3
=>x=6

bạn ko nên đăng linh tinh như thế nhé,nhưng dù sao thì hãy kết bạn vs mk vì mk cũng thích đá bóng(^_~) hihi



Ta có:
a/b =c/d
⟹a/c=b/d
Áp dụng tính chất dãy tỉ số bằng nhau ta có
a/c=b/d=5a+2b/5c+2b=5a-2b/5c-2d
Vì 5a=2b/5c=2d=5a-2b/5c-2d
⟹5a+2b/5a-2b=5c+2d/5c-2d
Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}.\)
\(\Rightarrow\frac{5a}{5c}=\frac{2b}{2d}.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{5a}{5c}=\frac{2b}{2d}=\frac{5a+2b}{5c+2d}\) (1)
\(\frac{5a}{5c}=\frac{2b}{2d}=\frac{5a-2b}{5c-2d}\) (2)
Từ (1) và (2) \(\Rightarrow\frac{5a+2b}{5c+2d}=\frac{5a-2b}{5c-2d}\)
\(\Rightarrow\frac{5a+2b}{5a-2b}=\frac{5c+2d}{5c-2d}\left(đpcm\right).\)
Chúc bạn học tốt!

Câu 1:
Quy tắc số cầu thủ ứng vs số áo của họ ko phải là 1 hàm số vì đại lượng cầu thr ko phải là các gt bằng số.
Câu 2:
Ta có:
\(P=x^3+x^2y-2x^2-xy-y^2+3y+x+2017\)
\(=x^2\left(x+y\right)-2x^2-y\left(x+y\right)+3y+x+2017\)
\(=2x^2-2x^2-2y+3y+x+2017\)
\(=x+y+2017\)
\(=2019\)
Vậy...........................

Giải tương tự như bài tập 59
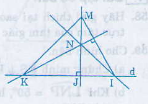
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK
Hướng dẫn:
Giải tương tự như bài tập 59

∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

?