Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

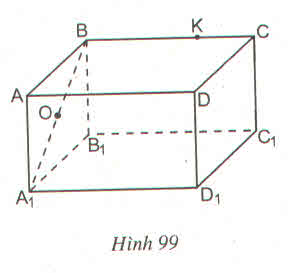
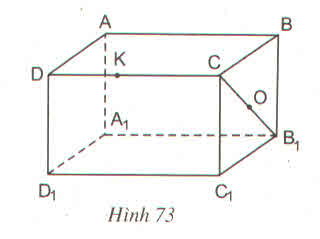
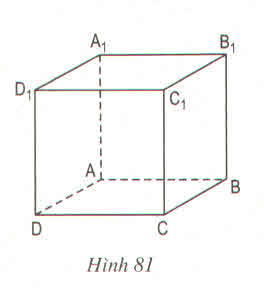
a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.

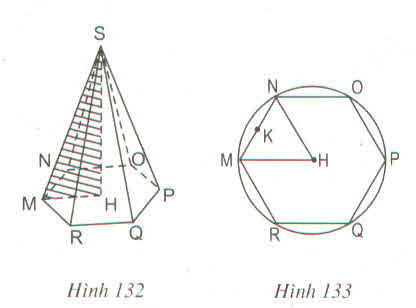
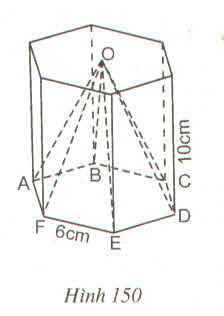
chia đáy hình chóp đều thành 6 phần bằng nhau
diện tích của 1 tam giác đều là : 1/2 . 6 . \(\sqrt{6^2-\left(\dfrac{1}{2}.6\right)^2}\)=3.\(\sqrt{27}\) (cm2
diện tích đáy của hình chóp là : 3.\(\sqrt{27}\).6=18.\(\sqrt{27}\) (cm2)
thể tích của hình chóp là : 1/3 . 18.\(\sqrt{27}\).10=180.\(\sqrt{3}\) (cm3)
vậy đáp án đúng là (C)180\(\sqrt{3}\) cm3

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ˆB=ˆD⇒B^=D^
Ta có ˆB+ˆD=3600−(100+60)=200B^+D^=3600−(100+60)=200
Do đó ˆB=ˆD=1000B^=D^=1000

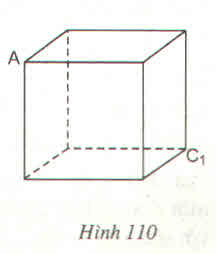
Với hình hộp chữ nhật ABCD. A 1B1C1D1
a) Nếu O là trung điểm của đoạn CB1 thì O cũng là trung điểm của đoạn C1B vì CBB1C1 là hình chữ nhật nên hai đường chéo có chung một trung điểm.
b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB1 vì bốn điểm C, D, B, B1 không thuộc một mặt phẳng

) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD




(C) \(\sqrt{32}\)m