Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

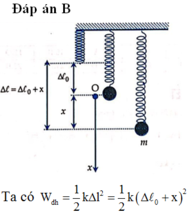
Từ đồ thị ta thấy
Vật nặng cao nhất lò xo biến dạng ![]() thế năng đàn hồi có giá trị tương ứng với 1 đơn vị chia trên trục tọa độ.
thế năng đàn hồi có giá trị tương ứng với 1 đơn vị chia trên trục tọa độ.
Vật nặng thấp nhất lò xo biến dạng ![]() thế năng đàn hồi có giá trị tương ứng với 9 đơn vị chia trên trục tọa độ
thế năng đàn hồi có giá trị tương ứng với 9 đơn vị chia trên trục tọa độ

![]()
Mặt khác 4 đơn vị chia ứng với 80 mJ. Vậy 1 đơn vị chia ứng với 20mJ ta được:

Mặt khác xét ở vị trí cân bằng: Ở vị trí cân bằng lực đàn hồi cân bằng với trọng lực nên:
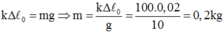

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

Chọn B.
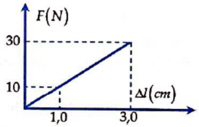
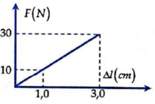
Đồ thị suy ra:
![]()
Độ dãn của lò xo khi lực đàn hồi bằng 25N:
![]()
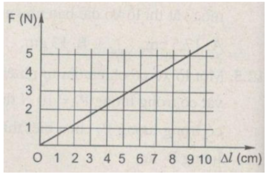
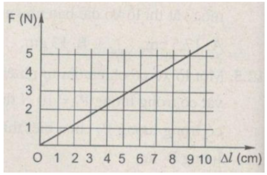
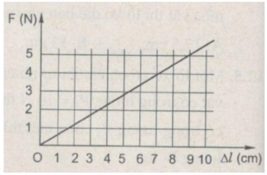


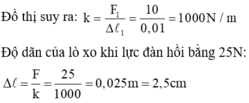
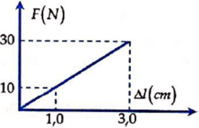

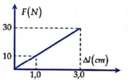
Vì F tỉ lệ thuận với ∆ l