Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ CQ vuông góc đường thẳng OA tại Q.
mà OB vuông góc OA (vì góc xOy vuông)
\(\Rightarrow OB\) song song CQ
\(\Delta ACQ\)có B là trung điểm AC
OB song song CQ (cmt)
\(\Rightarrow\)O là trung điểm AQ hay Q đối xứng A qua O
* VẬY bất kỳ vị trí của điểm B trên tia Ox thì điểm C luôn di chuyển trên đường thẳng đối xứng với A qua O và vuông góc với OA

A B C D E I K O M Q P
Lấy P và Q lần lượt là trung điểm của AB và AC. Nối M với I & K.
Xét \(\Delta\)BMD: ^BMD = 900; ^MBD = 450 => \(\Delta\)BMD vuông cân tại M
Ta thấy I là trung điểm BD => MI vuông góc góc với BD => ^MIA = 900
Tương tự: ^MKA = 900 . Xét tứ giác AIMK có: ^IAK = ^MIA = ^MKA = 900
=> Tứ giác AIMK là hình chữ nhật. Ta có: O là trung điểm của đường chéo IK
=> O là trung điểm AM.
Xét \(\Delta\)BAM: P là trung điểm AB; O là trung điểm AM => OP là đg trung bình \(\Delta\)BAM
=> OP // BM hay OP // BC. Tương tự: OQ // BC => 3 điểm P;O;Q thẳng hàng (Theo tiên đề Ơ-clit)
=> O nằm trên đường trung bình PQ của \(\Delta\)ABC
Vậy khi M chạy trên cạnh BC của \(\Delta\)ABC thì trung điểm O của IK di động trên đg trung bình của \(\Delta\)ABC.

bạn ơi sao mk vẽ hình thì nó lại ra góc bẹt lun chứ ko tạo ra 1 tam giác
bạn vẽ hình giúp mk nhé

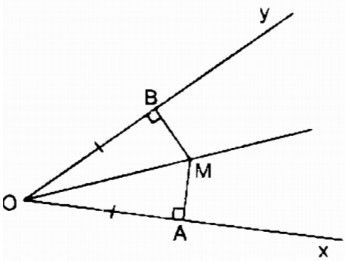
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
y x B K O C1 z A H C
a)Phần thuận:
Dựng CH, CK lần lượt vuông góc với Ox, Oy thì tam giác vuông CAH = tam giác vuông CBK =>CH=CK.
Mặt khác góc xOy cố định =>C thuộc tia phân giác Oz của góc xOy
b) giới hạn, phần đảo:
c) Kết luận: Tập hợp điểm C là tia phân giác Oz của góc xOy