Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

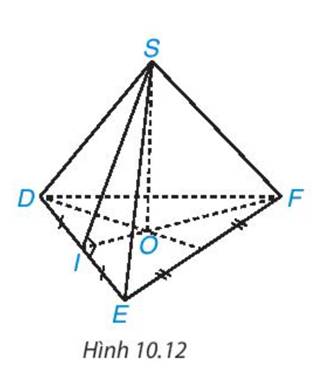
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

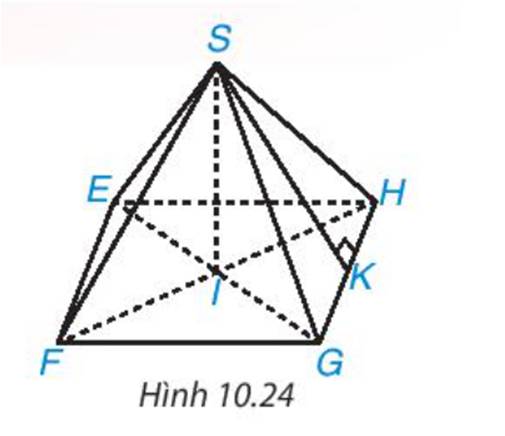
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

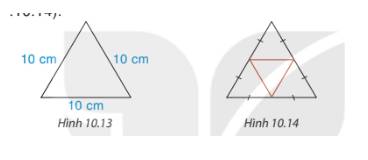
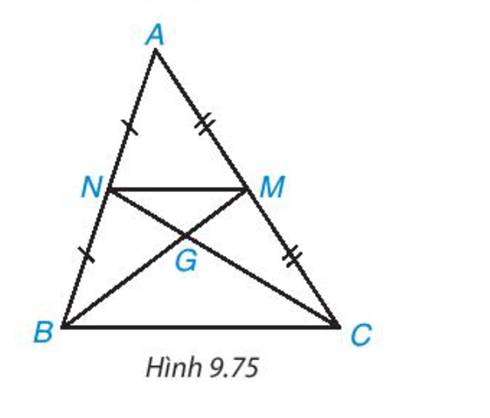
- Xét tam giác ABC có, NA=NB, MA=MC
=> NM là đường trung bình của tam giác ABC
=> NM // BC, \(NM = \frac{1}{2}AB\)
- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC

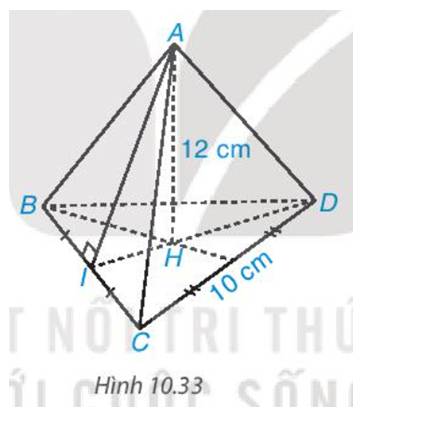
- Xét tam giác BID vuông tại I, có
\(I{{\rm{D}}^2} = B{{\rm{D}}^2} - B{I^2} = {10^2} - {5^2}\)
=> ID ≈ 8,66 (cm)
- Diện tích tam giác BCD là:
\({S_{BC{\rm{D}}}} = \frac{1}{2}.I{\rm{D}}.BC = \frac{1}{2}.8,66.10 = 43,3\left( {c{m^2}} \right)\)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.43,3.12 \approx 173,2(c{m^3})\)

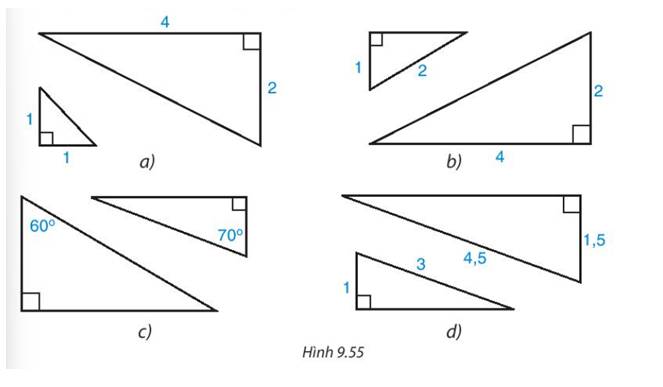
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

Nửa chu vi của hình tam giác đều ABC là:
\(p = \frac{1}{2}\left( {60 + 60 + 60} \right) = 90(cm)\)
Diện tích xung quanh của hình chóp tam giác đều S. ABC là:
\({S_{xq}} = 90.90 = 8100(c{m^2})\)
Vậy diện tích các mặt bên của hình chóp tam giác đều là 8100 cm2

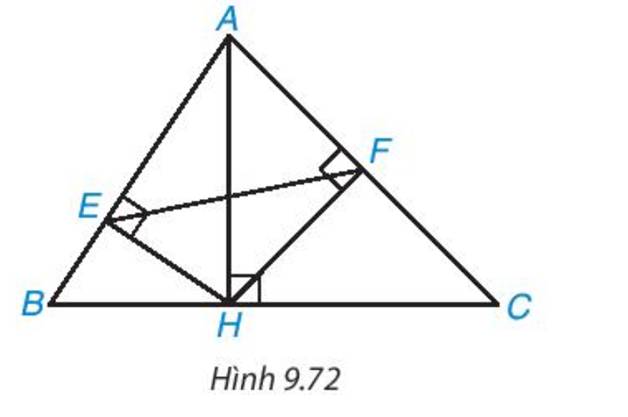
a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có: góc A chung
=> ΔAEH ∽ ΔAHB
b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có: góc A chung
ΔAFH ∽ ΔAHC
c) Vì ΔAEH ∽ ΔAHB nên:
\(\frac{{A{\rm{E}}}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{\rm{E}} = \frac{{A{H^2}}}{{AB}}\) (1)
Vì ΔAFH ∽ ΔAHC nên:
\(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF = \frac{{A{H^2}}}{{AC}}\)(2)
Từ (1) và (2) ta có:
\[\frac{{A{\rm{E}}}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]
Xét hai tam giác ΔAFE và ΔABC có:
Góc A chung
\[\frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]
Suy ra ΔAFE ∽ ΔABC (c.g.c)
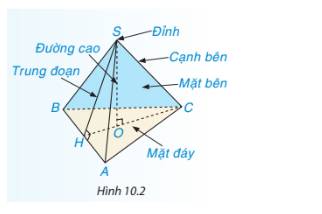
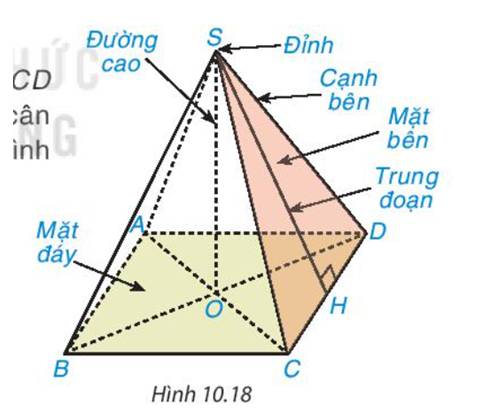
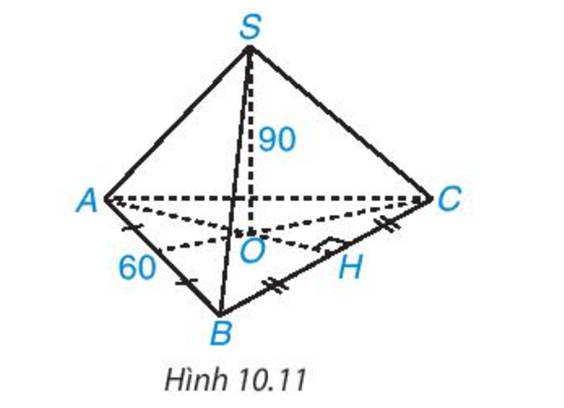
Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH