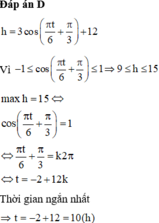Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(h=3cos\left(\dfrac{\pi t}{6}+\dfrac{\pi}{3}\right)+12\le3.1+12=15\left(m\right)\)
" = " \(\Leftrightarrow\dfrac{\pi t}{6}+\dfrac{\pi}{3}=2k\pi\left(k\in Z\right)\) \(\Leftrightarrow\dfrac{t}{6}+\dfrac{1}{3}=2k\Leftrightarrow t=12k-2\)
t min ; t > 0 \(\Rightarrow k=1\) thì t = 10 (h)

+) Độ sâu của mực nước là 15m thì h = 15.
Khi đó
\(\begin{array}{l}15 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos 0\\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi - 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {2\pi - 1} \right)}}{\pi };\frac{{6\left( {4\pi - 1} \right)}}{\pi }} \right\}\)
+) Độ sâu của mực nước là 9m thì h = 9.
Khi đó
\(\begin{array}{l}9 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = - 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \pi \\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = \pi + k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi + \pi - 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi + \pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 1\end{array}\)
Lại do \(k \in Z \Rightarrow k = 1 \Rightarrow t = \frac{{6\left( {3\pi - 1} \right)}}{\pi }\)
+) Độ sâu của mực nước là 10,5m thì h = 10,5.
Khi đó
\(\begin{array}{l}10,5 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = - \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \frac{{2\pi }}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{{\pi t}}{6} + 1 = \frac{{2\pi }}{3} + k2\pi \\\frac{{\pi t}}{6} + 1 = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\\t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\end{array} \right.\end{array}\)
Với \(t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 \le k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {0;1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {\frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{8\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{14\pi }}{3} - 1} \right)}}{\pi }} \right\}\)
Với \(t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( { - \frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{4\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{10\pi }}{3} - 1} \right)}}{\pi }} \right\}\)

Lời giải:
$\sin (\frac{\pi t}{18}-\frac{\pi}{6})\leq 1$ với mọi $t\in [0;24]$
$\Rightarrow h\leq 2.1+5=7$
Vậy $h_{\max}=7\Leftrightarrow \sin (\frac{\pi t}{18}-\frac{\pi}{6})=1$
$\Leftrightarrow \frac{\pi t}{18}-\frac{\pi}{6})=\frac{\pi}{2}+2k\pi$ với $k$ nguyên
$\Leftrightarrow \frac{t}{18}-\frac{1}{6}=\frac{1}{2}+2k$ với $k$ nguyên
$\Leftrightarrow t=12+36k$ với $k$ nguyên.
Do $t\in [0;24]$ nên $t=12$
Đáp án C.

a) Tại thời điểm t = 2 độ sâu của nước là: \(h\left( 2 \right) = 0,8cos0,5.2 + 4 \approx 4,43{\rm{ }}m.\)
Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.
b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình \(0,8cos0,5t + 4 = 3,6\).
Ta có: \(0,8cos0,5t + 4 = 3,6\)
\(\begin{array}{l} \Leftrightarrow cos0,5t = - \frac{1}{2} = cos\frac{{2\pi }}{3}\\ \Leftrightarrow 0,5t = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\\ \Leftrightarrow t = \pm \frac{{4\pi }}{3} + k4\pi ,k \in \mathbb{Z}\end{array}\)
Với \(t = \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow - 0,3 \le k \le 0,62 \Rightarrow k = 0. \Rightarrow t = \frac{{4\pi }}{3}\)
Với \(t = - \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le - \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow 0,3 \le k \le 1,28 \Rightarrow k = 1 \Rightarrow t = - \frac{{4\pi }}{3} + 4\pi = \frac{{8\pi }}{3}\)
Vậy tại các thời điểm \(t = \frac{{4\pi }}{3}\), \(t = \frac{{8\pi }}{3}\) giờ thì tàu có thể hạ thủy.

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)