Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Giả sử chúng ta gặp nhau ở li độ x1, sau nửa chu kì thì chúng lại gặp nhau ở li độ -x1. Khoảng thời gian hai lần liên tiếp gặp nhau T/2.

Đáp án A
Vòng tròn đơn vị:
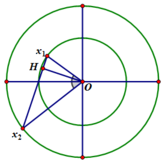
Để 2 vật ngang nhau thì OH phải trùng trục hoành. 2 lần liên tiếp OH trùng trục hoành cách nhau đúng nửa chu kỳ T/2.

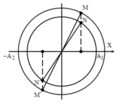
+ Hai vật có li độ ngang nhau khi hình chiếu vị trí của chúng trên trục hoành trùng nhau.
+ Dựa vào giản đồ vecto ta có thể thấy được khoảng thời gian 2 lần liên tiếp chúng trùng nhau là T 2
Đáp án A

Dao động tổng hợp x = x1 + x2
+ Khi x2 = 0 thì x1 = x - x2 = \(-5\sqrt{3}\)
+ Khi x1 = - 5 thì x2 = x - x1 = -2 + 5 = 3
Giả sử pt \(x_1=10\cos\left(\omega t\right)\) thì \(x_2=A_2\cos\left(\omega t+\varphi\right)\) (với \(\left|\varphi\right|<\frac{\pi}{2}\))
Theo giả thiết ta có:
\(\begin{cases}10\cos\left(\omega t\right)=-5\sqrt{3}\\A_2\cos\left(\omega t+\varphi\right)=0\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t\right)=-\frac{\sqrt{3}}{2}\\\cos\left(\omega t+\varphi\right)=0\end{cases}\)
cos O M1 M2 -√3/2 60°
Do \(\left|\varphi\right|<\frac{\pi}{2}\) nên ta chỉ có trường hợp như hình trên thỏa mãn, nghĩa là ta tìm đc \(\varphi=-\frac{\pi}{3}\)
Mặt khác: \(\begin{cases}10\cos\left(\omega t'\right)=-5\\A_2\cos\left(\omega t'+\varphi\right)=3\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t'\right)=-\frac{1}{2}\\\cos\left(\omega t'+\varphi\right)=\frac{3}{A_2}\end{cases}\)
Cũng biểu diễn trên đường tròn lượng giác như trên, ta được
cos O M1 M2 -1/2 1/2
\(\Rightarrow A_2=6cm\)
Biên độ tổng hợp:
\(A^2=10^2+6^2+2.10.6.\cos\frac{\pi}{3}\Rightarrow A=14\)cm.

Mình nghĩ là đáp án a chứ bạn,vì đồng biến hay nghịch biến tức là ta xét đến việc cùng tăng hay cùng giảm giá trị chứ không phải cùng hay trái dấu đâu
Theo định luật II Newton: \(\vec{a}=\dfrac{\vec{F}}{m}\)
Về độ lớn: \(a=\dfrac{F}{m}\)
Như vậy, a tỉ lệ thuận với F, và quan hệ là đồng biến.

Chọn đáp án A
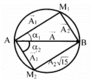
Từ giản đồ ta có: A 1 = A 2
Dựa vào tam giác vuông ∆ A M 2 B . Ta có: A 2 2 + 15 A 2 2 = 16 ⇒ A 2 = 4 c m


Đáp án A
Biểu diễn hai vị trí tương ứng trên đường tròn, ta dễ dàng xác định được △ φ = π 2