Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chú ý trong mạch dao động \(i_1\perp u_1;i_2\perp u_2\)
Mặt khác ta có độ lệch pha giữa hai \(i_1;i_2\):\(t_2-t_1=\frac{\pi}{2}\sqrt{LC}=\frac{T}{4}\Rightarrow\Delta\varphi=\frac{T}{4}.\frac{2\pi}{T}=\frac{\pi}{2}\)
=> \(i_1\perp i_2\)
i i u u 1 1 2 2
Nhìn vào đường tròn ta thấy \(i_1\perp i_2,u_1\perp u_2\); \(i_1\) ngược pha \(u_2\) và ngược lại.
\(\frac{i_1^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{i^2_2}{I_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{u^2_2}{U_0^2}=1;\frac{i_2^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\)
\(U_0=\frac{I_0}{\omega}\Rightarrow I_0=\omega\sqrt{U_0}=\frac{1}{\sqrt{LC}}\sqrt{U_0}\)
Dựa vào các phương trình trên ta thấy chỉ có đáp án D là sai.
Xem t = 0 là lúc cả hai mạch bắt đầu dao động
Phương trình hiệu điện thế trên 2 tụ C1 và C2 lần lượt có dạng
\(\begin{cases}u_1=12cos\left(\omega t\right)\left(V\right)\\u_2=6cos\left(\omega t\right)\left(V\right)\end{cases}\)
Độ chênh lệch Hiệu điện thế: \(\Delta u=u_1-u_2=6cos\left(\omega t\right)\left(V\right)\)
\(u_1-u_2=6cos\left(\omega t\right)=\pm3\Rightarrow cos\left(\omega t\right)=\pm0,5\Rightarrow cos\left(\frac{2\pi}{T}t\right)=\pm0,5\)
\(\Rightarrow\Delta t_{min}=\frac{T}{6}=\frac{10^{-6}}{3}s\)
Sử sụng hệ thức: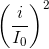 
+
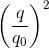= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =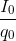 
= 50 (rad/s)
Khoảng thời gian để \(W_C=W_L\) giữa hai lần liên tiếp là \(\frac{T}{4}s\)
\(=> \frac{T}{4}=10^{-6}s=> T= 4.10^{-6}s.\)
\(W=\frac{1}{2}CU_0^2=> C = 1,25.10^{-7}F. \)
\(T=2\pi \sqrt{LC}=> L = \frac{T^2}{4\pi^2 C}=3,2.10^{-6}H.\)
\(W=\frac{1}{2}LI_0^2=> I_0=0,79A.\)
Do giá trị hiệu dụng I1 = I2
nên Z1 = Z2
Ta có thể biểu diễn Z trên giản đồ như thế này.
i Z1 Z2 α α
Chiều của Z chính là chiều của điện áp u
+ So với i1 thì pha ban đầu của u là: \(\frac{\pi}{4}-\alpha\)
+ So với i2 thì pha ban đầu của u là: \(-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\frac{\pi}{4}-\alpha=-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\alpha=\frac{\pi}{6}\)
\(\Rightarrow\varphi_u=\frac{\pi}{4}-\frac{\pi}{6}=\frac{\pi}{12}\)
Vậy \(u=60\sqrt{2}\cos\left(100\pi t+\frac{\pi}{12}\right)V\)
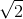
Do \(i,q\) trong mạch LC dao động vuông pha với nhau nên ta có phương trình
\(\frac{q_1^2}{Q_{01}^2} + \frac{i_1^2}{I_{01}^2} = 1\) => \( \frac{i_1^2}{I_{01}^2} = 1-\frac{q_1^2}{Q_{01}^2}.(1)\)
\(\frac{q_2^2}{Q_{02}^2} + \frac{i_2^2}{I_{02}^2} = 1\)=> \(\frac{i_2^2}{I_{02}^2} = 1-\frac{q_2^2}{Q_{02}^2} .(2)\)
do tại thời điểm t có \(Q_{01} = Q_{02} = Q_0; q_1 = q_2= q\)
\(I_{01} = Q_0.\omega_1; I_{02} = Q_0\omega_2\)
Lấy \((1)\) chia cho \((2)\) ta được: \(\frac{i_1^2I_{02}}{i_2^2I_{01}} = 1\)
=> \(\frac{i_1}{i_2} = \frac{I_{01}}{I_{02}}= \frac{\omega_1}{\omega_2} = \frac{T_2}{T_1} =3.\)
Chọn đáp án.D.3
Mình gõ nhâm dòng thứ 6: Sửa lại
\(\frac{i_1^2I_{02}^2}{i_2^2I_{01}^2} = 1\)