Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác APB và AQB, ta có:
\(\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}}\) và \(\tan {48^ \circ } = \frac{{AB}}{{QB}}\)
\(\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}\)
Mà \(AB = \tan {48^ \circ }.QB\)
\( \Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)\)
Vậy tháp hải đăng cao khoảng 568,5 m.

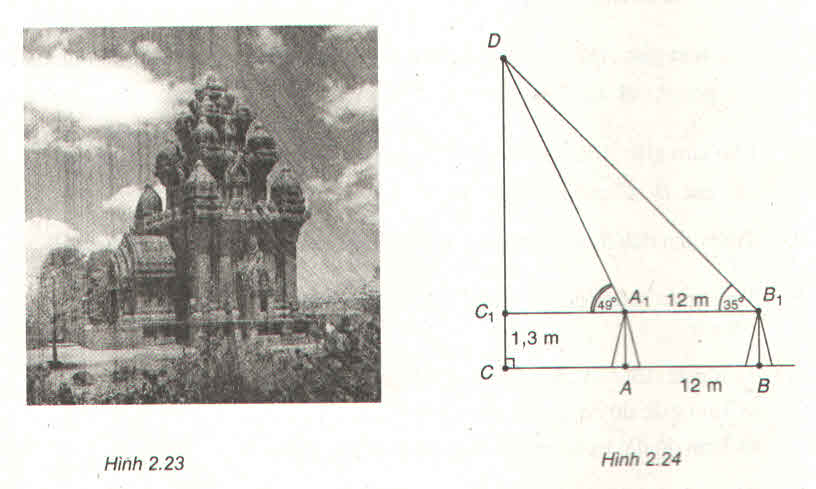
Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 + 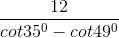
=> DC ≈ 22,8m
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com

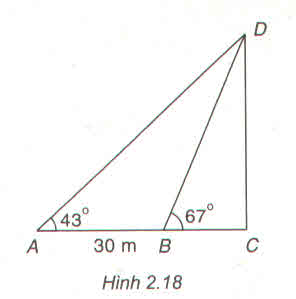
Có:
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.
Hai chiếc tàu thủy P và Q cách nhau 300m.TỪ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc
#Hỏi cộng đồng OLM
#Toán lớp 10

Ta có: AQ = ABcot480
AP = ABcot350
QP = AB(cot350 – cot480)

=> AB = ≈
Tính được AB ≈ 568,50m

Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
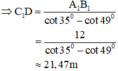
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.

Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)

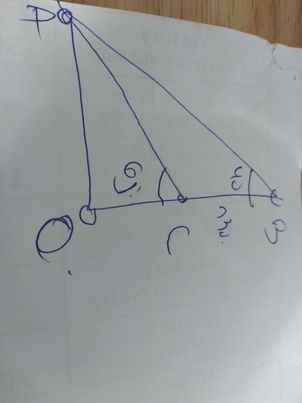
Kẻ AO vuông góc với BC tại O
=>OC là độ cao của ngọn đồi
\(\widehat{ACO}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+65^0=180^0\)
=>\(\widehat{ACB}=115^0\)
Xét ΔACB có \(\widehat{ACO}\) là góc ngoài tại C
nên \(\widehat{ACO}=\widehat{CAB}+\widehat{CBA}\)
=>\(\widehat{CAB}+40^0=65^0\)
=>\(\widehat{CAB}=25^0\)
Xét ΔCAB có
\(\dfrac{BA}{sinACB}=\dfrac{BC}{sinBAC}\)
=>\(\dfrac{BA}{sin115}=\dfrac{130}{sin25}\)
=>\(BA=\dfrac{130}{sin25}\cdot sin115\simeq278,79\left(m\right)\)
Xét ΔBOA vuông tại O có \(cosABO=\dfrac{BO}{BA}\)
=>\(\dfrac{BO}{278.79}=cos40\)
=>\(BO=278,79\cdot cos40\simeq213,57\left(m\right)\)
BO=BC+CO
=>CO+130=213,57
=>CO=83,57(m)
Vậy: Độ cao của ngọn đồi là 83,57 mét


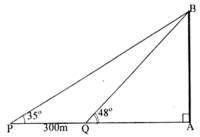


Ta có: AQ = ABcot480
AP = ABcot350
QP = AB(cot350 - cot480)
=> AB =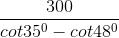 ≈
≈ 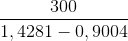
Tính được AB ≈ 568,50m