Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình tự vẽ
a) Ta có :
AG = GD . Mà GM = \(\frac{1}{2}\) AG
=> GD = \(\frac{1}{2}\) AG
Do AG = \(\frac{1}{3}\) AM
=> GD = \(\frac{2}{3}\) AM (*)
Xét tứ giác GBDC ta có:
BM = MC ( gt ) (1)
GM= MD ( do GD = \(\frac{1}{2}\) AG ) (2)
Từ (1)(2) => Tứ giác GBDC là hình bình hành
=> GC// và =BD ; BG // và =DC
Xét tam giác ABD ta có:
AP = P B ( gt ) ( 3)
AG = GD ( gt ) (4)
Từ (3)(4) => PG là đường trung bình của tam giác ABD
=> PG = \(\frac{1}{2}\)BD .Do BD = GC => PG=\(\frac{1}{2}\)GC
Mà PG = \(\frac{1}{3}\)PC => GC =\(\frac{2}{3}\)PC(**)
Chứng mình tương tự . Xét tam giác ADC ( làm tường tự cái trên nha )
=> NG=\(\frac{2}{3}\)BN (***)
Từ (*)(**)(***) => Đpcm
b) Xét tam giác DBA ta có :
AG = GD ( gt )
BF=FD ( gt )
=> GF là đường trung bình bình của tam giác DAB
=> GF = \(\frac{1}{2}\)AB( 5)
Ta có : DC = GB ( cm ở câu a )
Do BE = EG ; BG =\(\frac{2}{3}\)BN ( cm ở câu a)
=> EN = BG => EN= DC
Mà BG// DC ( cm ở câu a)
=> tứ giác ENCD là hình bình hành ( 1 cặp cạnh // và bằng nha )
=> DE=NC
Mà NC =\(\frac{1}{2}\)AC (6)
=> AN= NC
Ta lại có BM=MC ( gt) => BI=\(\frac{1}{2}\)BC (7)
Từ (5)(6)(7) => Đpcm
a) Do G là trọng tâm của tam giác ABC nên :
\(\dfrac{BG}{BN}=\dfrac{2}{3};\dfrac{GM}{AG}=\dfrac{1}{2}\)Do G là trung điểm của AD NÊN\(\dfrac{GD}{AG}=1\)
\(\Rightarrow GM=MG\) . \(\Rightarrow\dfrac{GD}{AG}=\dfrac{2}{3}\)
Tự cm \(\Delta BMD=\Delta CMG\left(c-g-c\right)\)
=> \(GC=BD\) Mà \(\dfrac{GC}{QC}=\dfrac{2}{3}\) \(\Rightarrow\dfrac{BD}{QC}=\dfrac{2}{3}\)
Vậy \(\dfrac{BG}{BN}=\dfrac{2}{3};\dfrac{BD}{QC}=\dfrac{2}{3};\dfrac{GD}{AG}=\dfrac{2}{3}\)
b) ta có luôn \(BM=\dfrac{1}{2}BC\left(gt\right)\)
Tự chứng minh KG là đường trung bình của Tam giác ABD
=> \(KG=\dfrac{AB}{2}\)
HN = BG = DC ; HN // CD (tự chứng minh ) => \(HD=NC=\dfrac{1}{2}AC\)
Vậy .......
a) Theo định lí pytago vào tam giác ABC:
BC2=AB2+AC2
=>BC^2=9^2+12^2
=>BC^2=81+144
=>BC^2=225
=>BC^2=căn 225=15 cm.(theo giả thiết cho cũng bằng 15 cm)
Vậy tam giác ABC vuông tại A
b) Vì MH=MK mà MH vuông góc với AC, MK là tia đối của MH nên tam giác KMB vuông tại K
Xét 2 tam giác MHC và MKB có:
MH = MK theo giả thiết
MB = MC vì AM là trung tuyến ứng với với BC
góc H = góc K = 90 độ
=> 2 tam giác trên bằng nhau.(cạnh huyền-cạnh góc vuông)
=> góc KMB = góc HMC.
Mặt khác, hai góc KMB và HMC ở vị trí so le trong nên BK//HC hay BK//AC.(còn một cách cm nữa)
c) Xét hai tam giác vuông MHA và MHC có:
MH chung
MA=MC vì AM là trung tuyến ứng với BC
góc MHA = góc MHC = 90 độ
=> tam giác MHA = tam giác MHC. (cạnh huyền - cạnh góc vuông)
=> HA=HC
=> H là trung điểm của BC
=> BH là trung tuyến ứng với AC
Vì AM, BC là các trung tuyến mà hai trung tuyến này(AM, BC) cắt tại G nên G là trọng tâm của tam giác ABC
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA =
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG'=
AM
Vì G là trọng tâm của ∆ABC => GB =
BN
Mặt khác : GM =
AG ( G là trọng tâm )
AG = GG '(gt)
GM =
GG '
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = GM '
MB = MC
=> BG '= CG
mà CG =
CE (G là trọng tâm ∆ABC)
=> BG =
EC
Vậy mỗi cạnh của ∆BGG' bằng
đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM =
BC
Vì IG =
BG (I là trung điểm BG)
GN =
BG ( G là trọng tâm)
=> IG = GN
Do đó ΔIGG '= ΔNGA (cgc) => IG' = AN => IG '=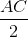
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE =
GC (G là trọng tâm ∆ABC)
=> GE =
BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=>
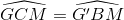(lại góc sole trong)
=> CE // BG' =>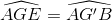
(đồng vị)
Làm Độ ΔAGE = ΔGG'K (CGC) => AE = GK
mà AE =
AB nên GK = 
AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó