K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
LA
9 tháng 1 2024
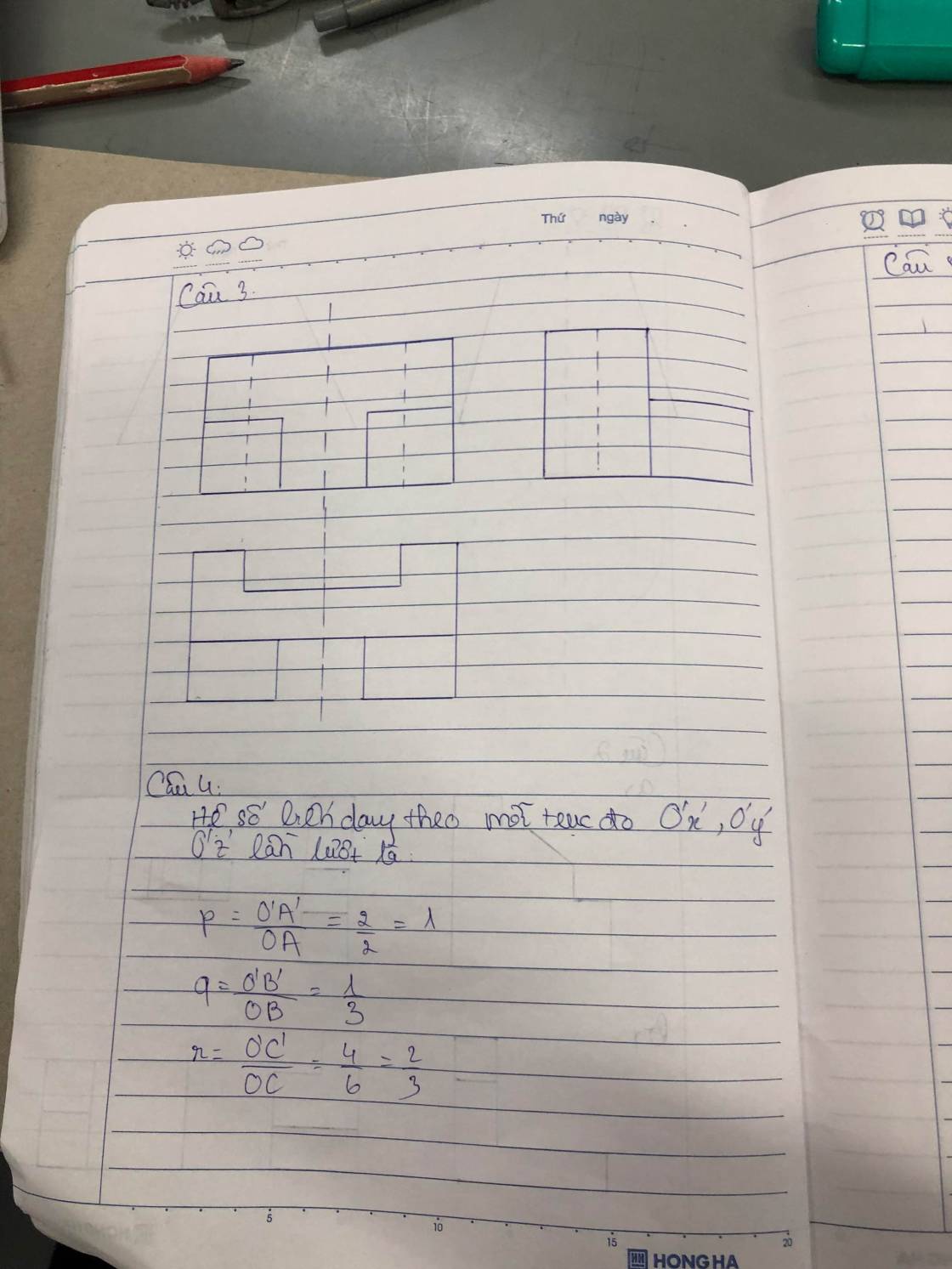
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
TD
9
TD
52
11 phút trước
Câu 1: \(\frac{\pi}{2}<\alpha,\beta<\pi\)
=>\(\sin\alpha>0;\sin\beta>0;cos\alpha<0;cos\beta<0\)
\(\sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\sin^2\alpha=1-\left(\frac13\right)^2=\frac89\)
mà \(cos\alpha<0\)
nên \(cos\alpha=-\frac{2\sqrt2}{3}\)
Ta có: \(\sin^2\beta+cos^2\beta=1\)
=>\(\sin^2\beta=1-\left(-\frac23\right)^2=1-\frac49=\frac59\)
mà \(\sin\beta>0\)
nên \(\sin\beta=\frac{\sqrt5}{3}\)
\(\sin\left(\alpha+\beta\right)=\sin\alpha\cdot cos\beta+cos\alpha\cdot\sin\beta\)
\(=\frac13\cdot\frac{-2}{3}+\frac{-2\sqrt2}{3}\cdot\frac{\sqrt5}{3}=\frac{-\sqrt2-2\sqrt{10}}{9}\)
Câu 2:
\(P=cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\frac12\cdot\left\lbrack cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right\rbrack=\frac12\cdot\left\lbrack cos2a+cos2b\right\rbrack\)
\(=\frac12\cdot\left\lbrack2\cdot cos^2a-1+2\cdot cos^2b-1\right\rbrack=cos^2a+cos^2b-1\)
\(=\left(\frac13\right)^2+\left(\frac14\right)^2-1=\frac19+\frac{1}{16}-1=\frac{25}{144}-1=-\frac{119}{144}\)
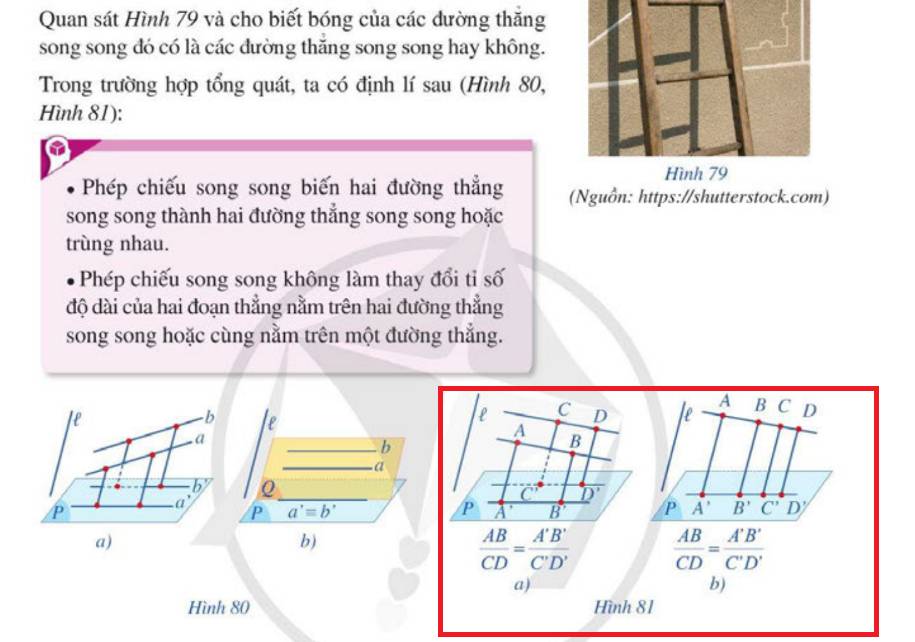
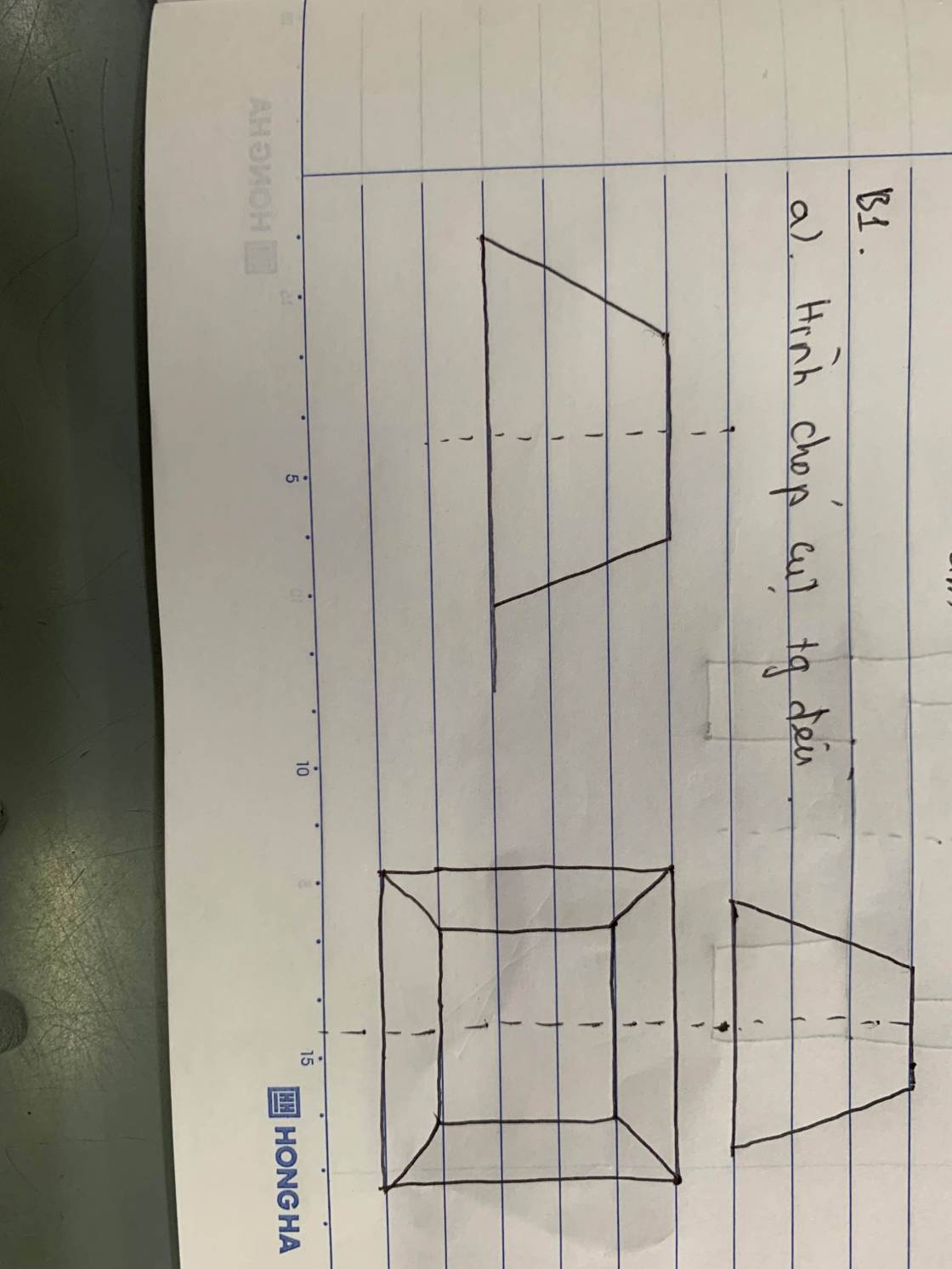
Ở hình a, em sử dụng 1 đường thẳng song song AB và CD qua B' và D' lần lượt cắt AA' và CC' tại E và F
Khi đó 2 tam giác A'B'E và C'D'F đồng dạng (3 cặp cạnh song song) nên dễ dàng suy ra đpcm
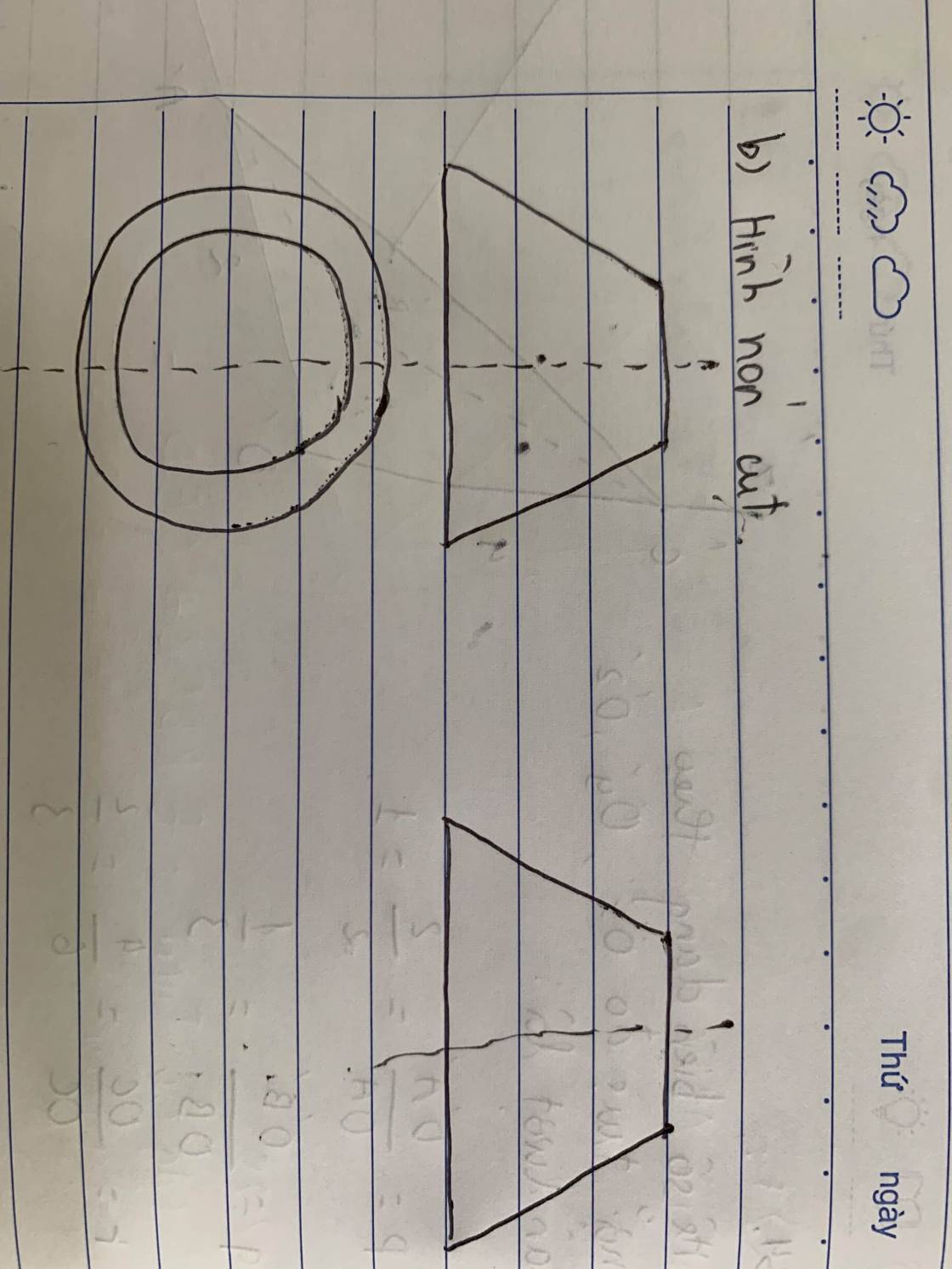
Hình b tương tự, chỉ cần qua D' kẻ 1 đường song song AD rồi lại đồng dạng là xong
Anh ơi, không biết em hiểu không đúng thì phải. Đường thẳng qua B' và D' // AB và CD. Nhưng B'D' và AB; CD chéo nhau ạ