K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
15 tháng 8
a: Xét ΔKAD và ΔBDA có
\(\hat{KAD}=\hat{BDA}\) (hai góc so le trong, AK//BD)
AD chung
\(\hat{KDA}=\hat{BAD}\) (hai góc so le trong, AB//CD)
Do đó: ΔKAD=ΔBDA
=>KA=BD
mà BD=AC
nên AK=AC
=>ΔAKC cân tại A
b: ΔAKC cân tại A
=>\(\hat{AKC}=\hat{ACK}\)
mà \(\hat{AKC}=\hat{BDC}\) (hai góc đồng vị, BD//AK)
nên \(\hat{BDC}=\hat{ACD}\)
Xét ΔBDC va ΔACD có
BD=AC
\(\hat{BDC}=\hat{ACD}\)
CD chung
Do đó: ΔBDC=ΔACD
=>\(\hat{BCD}=\hat{ADC}\)
=>ABCD là hình thang cân
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
22 tháng 3
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)
27 tháng 8
Ta có: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x^2+2xy+y^2\right)+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\begin{cases}x+y=0\\ x-1=0\\ y+1=0\end{cases}\Rightarrow\begin{cases}x=1\\ y=-1\end{cases}\)
Khi x=1;y=-1 thì ta có:
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}\)
=1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8
Olm chào em, khi đăng câu hỏi lên diễn đàn Olm, em cần đăng đầy đủ nội dung và yêu cầu, để nhận được sự trợ giúp tốt nhất từ cộng đồng Olm em nhé. Cảm ơn em đã đồng hành cùng Olm. Chúc em học tập hiệu quả và vui vẻ cùng Olm.
LN
5
15 tháng 8
bạn lưu ảnh rồi gửi qua file đi ạ chứ bn cóp sang thì ko hiện ảnh mất rồi
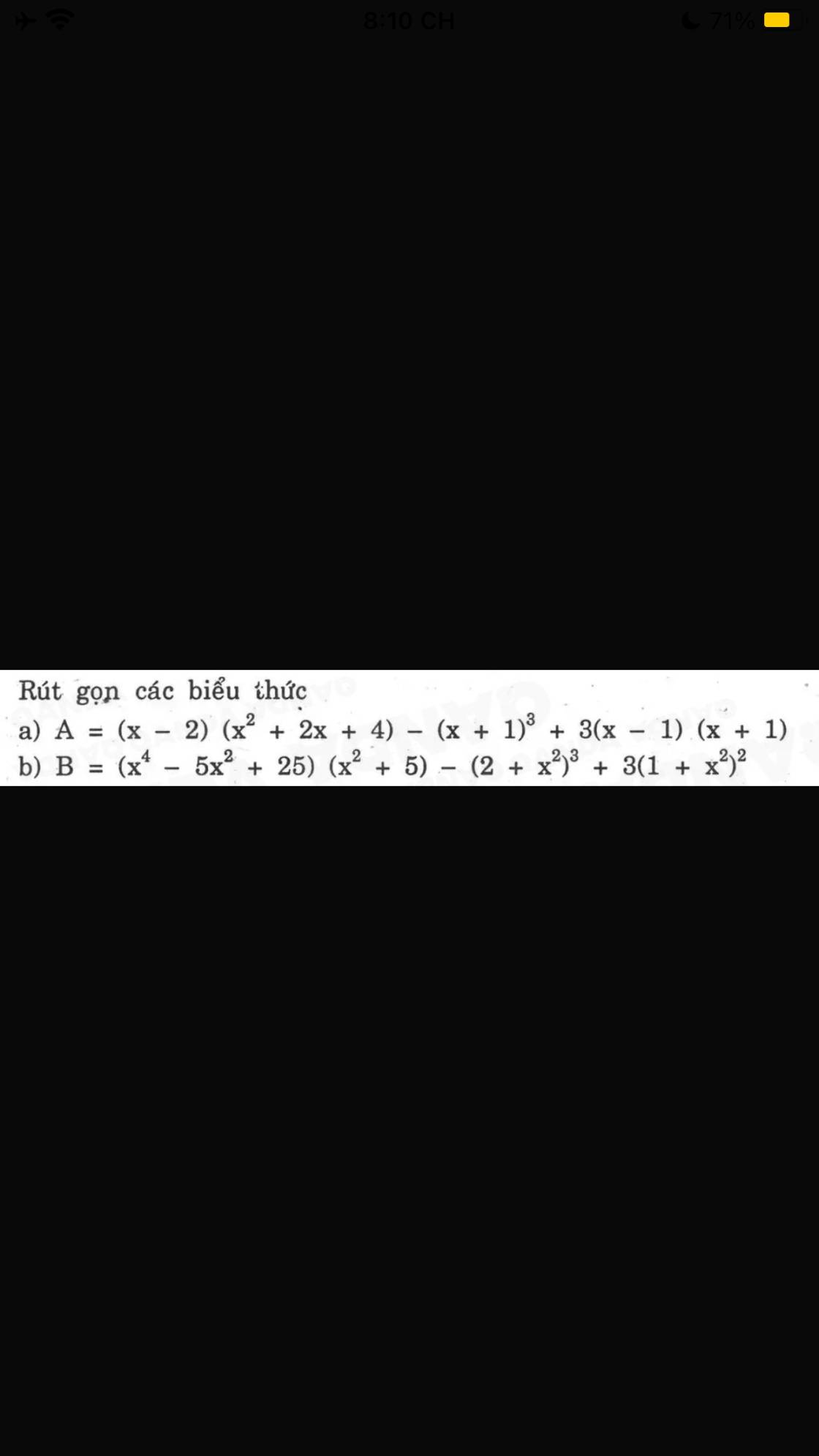
a: A=x^3-2^3+3x^2-3-(x^3+3x^2+3x+1)
=x^3+3x^2-11-x^3-3x^2-3x-1
=-3x-12
b: \(B=x^6+125-x^6-6x^4-12x^2-8+3\left(x^4+2x^2+1\right)\)
\(=-6x^4-12x^2+117+3x^4+6x^2+3\)
=-3x^4-6x^2+120