
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.
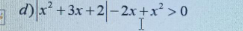 Giải bpt sau :
Giải bpt sau :





 giúp e với,sắp thi r
giúp e với,sắp thi r





 mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha
mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha

BPT\(\Leftrightarrow\left|x^2+3x+2\right|>2x-x^2\)
TH1:\(2x-x^2< 0\Leftrightarrow x\in R\backslash\left[0;2\right]\) (1)
TH2:\(\left\{{}\begin{matrix}2x-x^2\ge0\\\left(x^2+3x+2\right)^2>\left(2x-x^2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\\left(2x^2+x+2\right)\left(5x+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left[0;2\right]\\5x+2>0\end{matrix}\right.\)\(\Rightarrow x\in\left[0;2\right]\) (2)
Từ (1) (2) suy ra \(x\in R\)