Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) Góc ngoài còn lại: 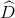 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 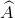 +
+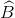 +
+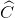 +
+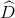 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Leftrightarrow\widehat{D}=360^o-\left(90^o+120^o+75^o\right)\)
\(\Leftrightarrow\widehat{D}=360^o-285^o=75^o\)
Ta có:+)\(\widehat{BAD}+\widehat{A_1}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{A_1}=180^o-\widehat{BAD}\)
\(\Rightarrow\widehat{A_1}=180^o-75^o=105^o\)
+)\(\widehat{B}_1+\widehat{CBA}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{CBA}\)
\(\Rightarrow\widehat{B_1}=180^o-90^0=90^o\)
\(+)\widehat{C_1}+\widehat{BCD}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{C_1}=180^o-\widehat{BCD}\)
\(\Rightarrow\widehat{C_1}=180^o-120^o=60^o\)
\(+)\widehat{D_1}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{D}_1=180^o-\widehat{ADC}\)
\(\Rightarrow\widehat{D_1}=180^o-75^o=105^o\)
b,Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}+\widehat{D_1}\)
\(=\left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\)
\(=180^o.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(=720^o-360^o=360^o\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^o\)

Đoạn thẳng f: Đoạn thẳng [A, D] Đoạn thẳng g: Đoạn thẳng [A, B] Đoạn thẳng j: Đoạn thẳng [B, C] Đoạn thẳng k: Đoạn thẳng [D, C] Đoạn thẳng l: Đoạn thẳng [A, C] Đoạn thẳng p: Đoạn thẳng [B, E] Đoạn thẳng q: Đoạn thẳng [D, F] Đoạn thẳng b: Đoạn thẳng [H, B] Đoạn thẳng c: Đoạn thẳng [D, K] Đoạn thẳng d: Đoạn thẳng [C, K] Đoạn thẳng e: Đoạn thẳng [H, C] Đoạn thẳng f_1: Đoạn thẳng [H, K] A = (3.41, -6.39) A = (3.41, -6.39) A = (3.41, -6.39) D = (29.5, -6.48) D = (29.5, -6.48) D = (29.5, -6.48) B = (12.08, 5.05) B = (12.08, 5.05) B = (12.08, 5.05) Điểm C: Giao điểm đường của h, i Điểm C: Giao điểm đường của h, i Điểm C: Giao điểm đường của h, i Điểm E: Giao điểm đường của m, l Điểm E: Giao điểm đường của m, l Điểm E: Giao điểm đường của m, l Điểm F: Giao điểm đường của n, l Điểm F: Giao điểm đường của n, l Điểm F: Giao điểm đường của n, l Điểm H: Giao điểm đường của r, t Điểm H: Giao điểm đường của r, t Điểm H: Giao điểm đường của r, t Điểm K: Giao điểm đường của s, a Điểm K: Giao điểm đường của s, a Điểm K: Giao điểm đường của s, a
1/ Xét tam giác ABE và CDF có:
\(\widehat{AEB}=\widehat{CFD}=90^o\)
AB = CD (Hai cạnh đối của hình bình hành)
\(\widehat{BAE}=\widehat{DCF}\) (So le trong)
nên \(\Delta ABE=\Delta CDF\) (Cạnh huyền - góc nhọn)
\(\Rightarrow BE=DF\)
Lại có BE và DF cùng vuông góc với AC nên BE // DF
Xét tứ giác BEDF có BE // DF và BE = DF nên BEDF là hình bình hành,
2/ Ta có do BC// AD nên \(\widehat{HBC}=\widehat{BAD}\) (Hai góc đồng vị)
Dó AB// CD nên \(\widehat{KDC}=\widehat{BAD}\) (Hai góc đồng vị)
Vậy nên \(\widehat{KDC}=\widehat{HBC}\)
Suy ra \(\Delta CHB\sim\Delta CKD\left(g-g\right)\Rightarrow\frac{CH}{CK}=\frac{CB}{CD}\Rightarrow\frac{CH}{CK}=\frac{CB}{AB}\)
Theo tính chất góc ngoài, ta có \(\widehat{ABC}=\widehat{BHC}+\widehat{HCB}=90^o+\widehat{HCB}\)
Do BC // AD; \(CK\perp AD\Rightarrow CK\perp BC\)
Suy ra \(\widehat{KCH}=\widehat{KCB}+\widehat{HCB}=90^o+\widehat{HCB}\)
Vậy \(\widehat{ABC}=\widehat{KCH}\)
Xét tam giác ABC và KCH có:
\(\widehat{ABC}=\widehat{KCH}\)
\(\frac{CH}{CK}=\frac{CB}{AB}\)
nên \(\Delta ABC\sim\Delta KCH\left(c-g-c\right)\)
*) Ta có \(\Delta ABE\sim\Delta ACH\left(g-g\right)\Rightarrow\frac{AB}{AC}=\frac{AE}{AH}\Rightarrow AB.AH=AC.AE\)
Tương tự \(\Delta AFD\sim\Delta AKC\left(g-g\right)\Rightarrow\frac{AF}{AK}=\frac{AD}{AC}\Rightarrow AD.AK=AC.AF\)
Suy ra \(AB.AH+AD.AK=AC.AE+AC.AF=AC\left(AE+AF\right)\)
Theo câu a, \(\Delta ABE=\Delta CDF\Rightarrow AE=CF\)
Vậy thì AE + AF = CF + AF = AC
Hay AB.AH + AD.AK = AC.AC = AC2

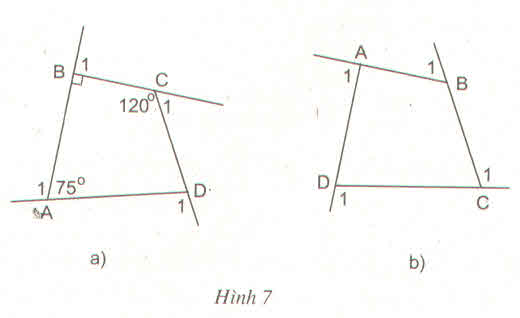
Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
\(\begin{array}{l}\widehat A + \widehat {{B_1}} + \widehat {{D_1}} = {180^o}\\\widehat C + \widehat {{B_2}} + \widehat {{D_2}} = {180^o}\end{array}\)
Khi đó, tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = \widehat A + \widehat {{B_1}} + \widehat {{D_1}} + \widehat C + \widehat {{B_2}} + \widehat {{D_2}} = 180^\circ + 180^\circ = 360^\circ \)
Vậy \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)

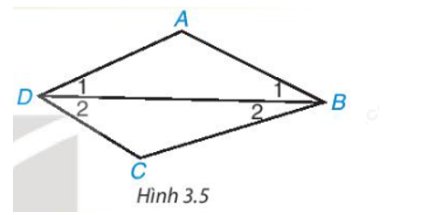
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).

Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)