PM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
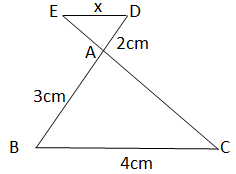
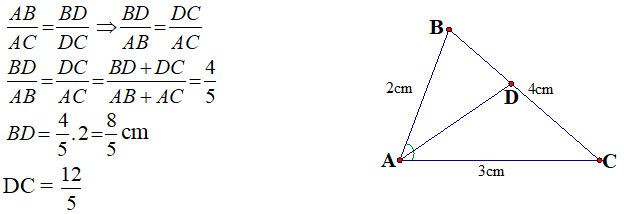
Ta có: \(BD+CD=BC=4\)
\(\Rightarrow BD=4-CD\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{4-CD}{2}=\dfrac{CD}{3}\)
\(\Rightarrow12-3CD=2CD\)
\(\Rightarrow CD=\dfrac{12}{5}\left(cm\right)\)
\(BD=4-CD=\dfrac{8}{5}\left(cm\right)\)
15 tháng 2 2018
Tự vẽ hình nhé trả lời hóng giao thừa thôi :))
vì BE vuông góc BD nên BE là đường phân giác ngoài của tam giác ABC.
theo tính chất đường phân giác (ngoài) ta có :
\(\frac{AE}{AB}=\frac{EC}{BC}\)\(\Rightarrow\)\(CE=\frac{AC.BC}{AB}\)
\(\Rightarrow\)\(CE=\frac{AE.2}{3}\)
\(\Rightarrow\)\(3CE=\left(CE+AC\right).2\)
\(\Rightarrow\)\(3CE=2CE+2AC\)
\(\Rightarrow\)\(CE=2.AC=6\left(cm\right)\)
A
14 tháng 2 2018
vì BE vuông góc BD nên BE là đường phân giác ngoài của tam giác ABC.
theo tính chất đường phân giác (ngoài) ta có :
\(\frac{\text{AE}}{\text{AB}}=\frac{\text{EC}}{\text{BC}}\)
\(\Leftrightarrow\text{CE= }\frac{\text{AE∗BC}}{\text{AB}}\)
\(\Leftrightarrow\text{CE=}\frac{\text{AE∗2}}{3}\)
\(\Leftrightarrow\)3CE= ( CE+AC)*2\(\Leftrightarrow\)3CE= 2CE +2AC
\(\Leftrightarrow\)CE= 2AC=6cm :| :| :-SS :-SS